Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\widehat{C}=\widehat{BAH}=90^O-\widehat{CAH}\)
\(\widehat{B}=\widehat{CAH}=90^O-\widehat{BAH}\)
b)Ta có:
\(\widehat{ADC}=\widehat{B}+\widehat{BAD}=\widehat{B}+\frac{\widehat{BAH}}{2}=\widehat{B}+\widehat{\frac{C}{2}}\)
Lại có:
\(\widehat{DAC}=180^O-\widehat{C}-\widehat{ADC}=180^O-\widehat{C}-\left(\widehat{B}+\widehat{\frac{C}{2}}\right)=\left(90^O-\widehat{B}\right)-\frac{\widehat{C}}{2}+\left(90^O-\widehat{C}\right)\)
\(=\widehat{C}-\widehat{\frac{C}{2}}+\widehat{B}=\widehat{B}+\frac{\widehat{C}}{2}\)
Suy ra:\(\widehat{ADC}=\widehat{DAC}\)
\(\Rightarrow\Delta ADC\)cân tại C
c)\(DK\perp BC;AH\perp BC\Rightarrow DK//AH\)
\(\Rightarrow\widehat{KDA}=\widehat{DAH}\)(hai góc so le trong)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{BAD}=\widehat{KDA}\)
\(\Rightarrow\)\(\Delta KAD\)cân tại K
d)Xét \(\Delta CDK-\Delta CAK\)
\(\hept{\begin{cases}CD=CA\\KD=KA\\CA.chung\end{cases}}\)
\(\Rightarrow\Delta CDK=\Delta CAK\left(c.c.c\right)\)
\(\Rightarrowđpcm\)
e)Xét\(\Delta AID-\Delta AHD\)
\(\hept{\begin{cases}AI=AH\\AD.chung\\\widehat{DAI}=\widehat{DAH}\end{cases}}\)
\(\Rightarrow\widehat{AID}=\widehat{AHD}=90^O\)
\(\Rightarrow DI\perp AB.Mà.AC\perp AB\)
\(\Rightarrow DI//AC\)

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm

mik làm lại cho nó lq được ko?
a) ta xét t/gABM và t/gDBM ta có:
AB=DB (gt)
=>^ABM=^DBM
BM chung
=>t/gABM=t/gDBM (c.g.c)
b)Vì t/gABM=t/gDEM
=>AM=DM ( 2 cạnh tương ứng)
=>^MAD=^AMD=90o
=>MD_|_BC
c)Vì t/gABM=t/gDEM (đối đỉnh)
=>t/gAME=t/gDMC(cgv-gn)
=>ME=MC
=>t/gMEC cân tại M
=>^MEC=^MCE
Mà trong t/gMEC ta thấy:
^MEC+^MDA+^DAM=^MEC+^CEM+EMC
mà ^EMC=^AMD ( 2 góc đối đỉnh)
=>^MAD+^MDA=^MEC+^EMC
=>^MAD=^MCE ( so le)
=>AD//CE
=>đpcm.
A B C D E M
a) tam giác ABM=tam giác DBM (c.g.c) (1) suy ra AM=MD
b) Từ (1) suy ra góc BAM = góc BDM
mà góc BAM = 900
suy ra góc BDM = 900
suy ra MD vuông góc với BC tại D
c) Vì AB=BD suy ra tam giác ABD cân tại B
mà BM là phân giác của góc ABD
suy ra BM là phân giác đồng thời là đường cao của tam giác ABD
suy ra BM vuông góc với AD (3)
Xét tam giác AME và tam giác DMC
có góc MAE=góc MDC=900
AM=MD ( CMT)
góc AME=góc DMC ( đối đỉnh)
suy ra tam giác AME = tam giác DMC (g.c.g)
suy ra AE=DC
mà AB+AE=BE, BD+DC=BC lại có AB=BD
suy ra BC = BE suy ra tam giác EBC cân tại B
mà BM là phân giác của góc EBC
suy ra BM là phân giác đồng thời là đường cao của tam giác EBC
suy ra BM vuông góc với CE tại M (4)
Từ (3) và (4) suy ra AD//CE

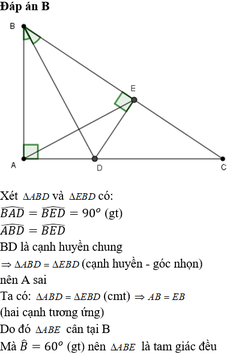
Hình (tự vẽ)
a) ΔABE cân
Xét hai tam giác vuông ABH và EBH có:
\(\widehat{ABH}=\widehat{EBH}\)(BH là phân giác)
HB là cạnh chung.
Do đó: ΔABH = ΔEBH (cạnh huyền - góc nhọn)
⇒ BA = BE (2 cạnh tương ứng)
⇒ ΔABE cân tại B.
b) ΔABE đều
Vì ΔABE là tam giác cân (câu a) có góc B bằng 60o (gt) ⇒ ΔABE là tam giác đều.
c) AED cân
Vì ΔABH = ΔEBH (câu a) ⇒ AH = EH (2 cạnh tương ứng)
Xét hai tam giác vuông ADH và EDH có:
AH = EH (cmt)
HD: cạnh chung
Do đó: ΔADH = ΔEDH (2 cạnh góc vuông)
⇒ \(\widehat{DAH}=\widehat{DEH}\)(góc tương ứng)
⇒ ΔAED cân tại D
d) ΔABF cân
Vì AF// HB ⇒ góc BAF = ABH = 30o (so le trong) (1)
Ta có: \(\widehat{ABC}+\widehat{ABF}=180^o\)(kề bù)
Thay: 60o + ABF = 180o
⇒ ABF = 180o - 60o = 120o
Xét ΔABF, ta có:
\(\widehat{ABF}+\widehat{BFA}+\widehat{FAB}=180^o\)(ĐL)
Thay: 120o + BFA + 30o = 180o
⇒ BFA = 180 - 120 - 30 = 30 (2)
Từ (1) và (2) suy ra: ΔABF cân tại B.

B2 : Hình dễ bạn tử kẻ hình nhá !
a)Ta có AH là đường cao
=> Góc AHB = AHC = 90o
Xết tam giác AHB có :
BAH + AHB + HBA = 180o ( tổng 3 góc trong 1 tam giác )
=> BAH + 90o + 70o =180o
=> BAH = 180o-70o-90o
=> BAH = 20o
Xét tam giác AHC cps :
AHC + HAC + HCA = 180o
=> 90 + HAC + 30 = 180
=> HAC = 180-30-90=60o
b) Ta có AD là đường phân giác
=> ABD= CAD = 80/2 = 40o
Xét tam giác ADB có :
ABD + BDA +DAB = 180
=> 70 + BDA + 40 = 180
=> BDA = 180-40-70 = 70
Xét tam giác ADC có :
ACD + CDA + DAC = 180
=> 30 + CDA + 40 = 180
=> CDA = 180-40-30
=> CDA=110
( **** )

a, Chứng minh tam giác ADB=tam giác ADC
=>góc BAD=góc CAD=>AD là tia phân giác của góc BAC=>góc BAD=góc CAD=10độ
b, Do tam giác ABC cân tại A và tam giác DCB đều nên góc ABC=(180độ-20độ):2= 80độ;góc DBC= 60độ
=> góc ABD=80 độ - 60 độ=20độ
Tia BM là tia phân giác của góc ABD=> góc ABM=góc DBM=10độ
Chứng minh được tam giác ABM = tam giác BAD(g.c.g) => AM=BD mà BD =BC nên AM=BC (đpcm)

A B C D E Vì \(\Delta ABC\)vuông tại A
Áp dụng Đ/lí py-tago
=>BC2=AB2+AC2
=>BC2=62+82=100
=>Bc=10
b)Dễ thấy tam giác ADB=tam giác ADE (Cạnh huyền-góc nhọn)
=>AD=AE
=>TAm giác ADE cân