Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

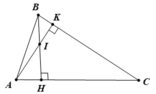
b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)

a. Hình vẽ ( 1 điểm)
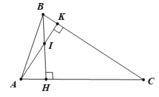
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)

Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)

+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)
góc A2 = xAC / 2
=> góc A2 = (góc ABC + C1) / 2 = B1 + ( C1 / 2 ) (Vì góc B1 = ABC /2 )
+) Trong tam giác AIB: góc AIB = 180o - (B1 + A1 + A2)
= 180o - (B1 + A1 +B1 + ( C1 / 2 ) )
= 180o - (2.B1 + A1 + ( C1 / 2 ) )
= 180o - (B + A1 + ( C1 / 2 ))
Mà B + A1 = 180o - C1 = 180o - 70o = 110o; C1 / 2 = 70o/ 2 = 35o
=> góc AIB = 180o - (110o + 35o) = 180o - 145o = 35o


+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)
góc A2 = xAC / 2
=> góc A2 = (góc ABC + C1) / 2 = B1 + ( C1 / 2 ) (Vì góc B1 = ABC /2 )
+) Trong tam giác AIB: góc AIB = 180o - (B1 + A1 + A2)
= 180o - (B1 + A1 +B1 + ( C1 / 2 ) )
= 180o - (2.B1 + A1 + ( C1 / 2 ) )
= 180o - (B + A1 + ( C1 / 2 ))
Mà B + A1 = 180o - C1 = 180o - 70o = 110o; C1 / 2 = 70o/ 2 = 35o
=> góc AIB = 180o - (110o + 35o) = 180o - 145o = 35o

Lời giải:
a) Áp dụng định lý tổng 3 góc trong một tam giác ta có:
$\widehat{AIC}=180^0-(\widehat{IAC}+\widehat{ICA})=180^0-\frac{\widehat{A}+\widehat{C}}{2}$
$=180^0-\frac{180^0-\widehat{B}}{2}=180^0-\frac{180^0-60^0}{2}=120^0$
b)
Xét tam giác $APK$ có $AH$ đồng thời là đường cao và đường phân giác nên $APK$ là tam giác cân tại $A$
Do đó: đường cao $AH$ đồng thời cũng là đường trung tuyến.
$\Rightarrow HK=\frac{1}{2}PK=\frac{1}{2}.6=3$ (cm)
Áp dụng định lý Pitago: $AK=\sqrt{AH^2+HK^2}=\sqrt{4^2+3^2}=5$ (cm)
c)
Kẻ phân giác $IT$ của $\widehat{AIC}$ thì $\widehat{AIT}=\widehat{CIT}=60^0$
$\widehat{AIE}=\widehat{CID}=180^0-\widehat{AIC}=60^0$
Xét tam giác $AEI$ và $ATI$ có:
$\widehat{EAI}=\widehat{TAI}$
$\widehat{AIE}=\widehat{AIT}=60^0$ (cmt)
$AI$ chung
$\Rightarrow \triangle AEI=\triangle ATI$ (g.c.g)
$\Rightarrow IE=TI(1)$
Tương tự: $\triangle CTI=\triangle CDI$(g.c.g)
$\Rightarrow TI=DI(2)$
$(1);(2)\Rightarrow IE=ID$ nên $IDE$ là tam giác cân tại $I$.

b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)