K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
0
H
31 tháng 3 2017
a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0
Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.
QD
31 tháng 3 2017
a) .
=
=
=
=
= 9.
b) :
=
=
=
=
=
= 8.
c) +
=
+
=
+
=
+
=
+
= 40.
d) -
=
-
=
-
=
-
= 121.
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
a) \(9^{\dfrac{2}{5}}.27^{\dfrac{2}{5}}=\left(9.27\right)^{\dfrac{2}{5}}=\left(3^2.3^3\right)^{\dfrac{2}{5}}=3^{5.\dfrac{2}{5}}=3^2=9\)
b) \(=\left(\dfrac{144}{9}\right)^{\dfrac{3}{4}}=\left(\dfrac{12}{3}\right)^{2.\dfrac{3}{4}}=4^{\dfrac{3}{2}}=2^{2.\dfrac{3}{2}}=2^3=8\)
c) \(=\left(\dfrac{1}{2}\right)^{4.\left(-0,75\right)}+\left(\dfrac{1}{4}\right)^{-\dfrac{5}{2}}\)
\(=\left(\dfrac{1}{2}\right)^{-3}+\left(\dfrac{1}{2}\right)^{-5}\)
\(=2^3+2^5=40\)
d) \(=\left(0,2\right)^{2.\left(-1.5\right)}-\left(0,5\right)^{3.\dfrac{-2}{3}}\)
\(=\left(\dfrac{1}{5}\right)^{-3}-\left(\dfrac{1}{2}\right)^{-2}\)
\(=5^3-2^2=121\)
Q
31 tháng 3 2017
- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
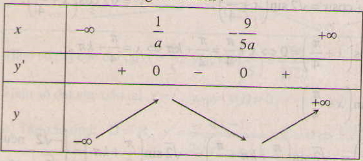
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
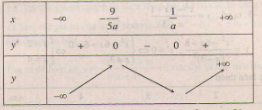
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.
Q
7 tháng 6 2017
a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)
QD
31 tháng 3 2017
a) ta có 2√5= = √20 ; 3√2 =
= √ 18 => 2√5 > 3√2
=> <
b) 6√3 = = √108 ; 3√6 =
= √54 => 6√3 > 3√6 =>
>
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
a) \(2\sqrt{5}=\sqrt{2^2.5}=\sqrt{20}\)
\(3\sqrt{2}=\sqrt{3^2.2}=\sqrt{18}\)
=> \(2\sqrt{5}>3\sqrt{2}\)
=> \(\left(\dfrac{1}{3}\right)^{2\sqrt{5}}< \left(\dfrac{1}{3}\right)^{3\sqrt{2}}\)
(vì cơ số \(\dfrac{1}{3}< 1\))
b) Vì \(3< 6^2\)
=> \(3^{\dfrac{1}{6}}< \left(6^2\right)^{\dfrac{1}{6}}\)
=> \(\sqrt[6]{3}< 6^{\dfrac{1}{3}}\)
=> \(\sqrt[6]{3}< \sqrt[3]{6}\)
=> \(7^{\sqrt[6]{3}}< 7^{\sqrt[3]{6}}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2018
\(\left(xy-1\right)2^{2xy-1}=\left(x^2+y\right)2^{x^2+y}\)
\(\Leftrightarrow\left(xy-1\right)2^{2\left(xy-1\right)+1}=\left(x^2+y\right)2^{x^2+y}\)
\(\Leftrightarrow2\left(xy-1\right)2^{2\left(xy-1\right)}=\left(x^2+y\right)2^{x^2+y}\)
Do vế phải luôn dương \(\Rightarrow VT>0\Rightarrow xy-1>0\) (1)
Xét hàm \(f\left(t\right)=t.2^t\) với \(t>0\Rightarrow f'\left(t\right)=2^t+t.2^t.ln2>0\)
\(\Rightarrow f\left(t\right)\) đồng biến \(\Rightarrow f\left(t_1\right)=f\left(t_2\right)\Leftrightarrow t_1=t_2\)
\(\Rightarrow2\left(xy-1\right)=x^2+y\Rightarrow2xy-y=x^2+2\) (thay \(x=\dfrac{1}{2}\) thấy ko phải nghiệm)
\(\Rightarrow y=\dfrac{x^2+2}{2x-1}\) (2)
Thay (2) vào (1): \(xy-1>0\Rightarrow x.\left(\dfrac{x^2+2}{2x-1}\right)-1>0\Rightarrow\dfrac{x^3+2x}{2x-1}-1>0\)
\(\Rightarrow\dfrac{x^3+1}{2x-1}>0\Rightarrow2x-1>0\) (do \(x>0\Rightarrow x^3+1>0\))
Vậy \(y=\dfrac{x^2+2}{2x-1}=\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{9}{4\left(2x-1\right)}=\dfrac{2x-1}{4}+\dfrac{9}{4\left(2x-1\right)}+\dfrac{1}{2}\)
\(\Rightarrow y\ge2\sqrt{\dfrac{\left(2x-1\right)}{4}.\dfrac{9}{4\left(2x-1\right)}}+\dfrac{1}{2}=2\)
\(\Rightarrow y_{min}=2\) khi \(\dfrac{2x-1}{4}=\dfrac{9}{4\left(2x-1\right)}\Rightarrow x=2\)
Đáp án B
=9
9