Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}

d) Phương trình đã cho tương đương với :
\(2^{3x}+2^x.3^{2x}=2.3^{2x}\Leftrightarrow\left(\frac{2}{3}\right)^{2x}+\left(\frac{2}{3}\right)^x-2=0\)
Đặt \(t=\left(\frac{2}{3}\right)^x,\left(t>0\right)\) Phương trình trở thành
\(t^3+t-2=0\) hay \(\left(t-1\right)\left(t^2+t+2\right)=0\)
Do \(t^2+t+2=\left(t+\frac{1}{2}\right)^2+\frac{7}{4}>0\) nên \(t-1=0\) hay t=1
Từ đó suy ra \(\left(\frac{2}{3}\right)^x=1=\left(\frac{2}{3}\right)^0\Leftrightarrow x=0\)
Vậy phương trình có nghiệm duy nhất \(x=0\)
c) Điều kiện \(x\ne0\). Chia cả 2 vế của phương trình cho \(6^{\frac{1}{x}}>0\), ta có :
\(6.\left(\frac{3}{2}\right)^{\frac{1}{x}}-13.1+6\left(\frac{2}{3}\right)^{\frac{1}{x}}=0\)
Đặt \(t=\left(\frac{3}{2}\right)^{\frac{1}{x}},\left(t>0\right)\)
Phương trình trở thành
\(6t-13+\frac{6}{t}=0\) hay \(6t^2-13t+6=0\)
Phương trình bậc 2 trên có 2 nghiệm dương \(t=\frac{3}{2},t=\frac{2}{3}\)
Với \(t=\frac{3}{2}\) thì \(\left(\frac{3}{2}\right)^{\frac{1}{x}}=\frac{3}{2}\Leftrightarrow\frac{1}{x}=1\Leftrightarrow x=1\)
Với \(t=\frac{2}{3}\) thì \(\left(\frac{3}{2}\right)^{\frac{1}{x}}=\frac{2}{3}\Leftrightarrow\frac{1}{x}=-1\Leftrightarrow x=-1\)





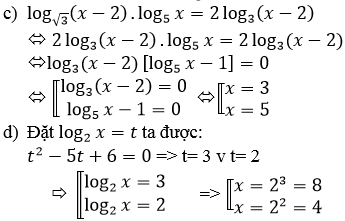
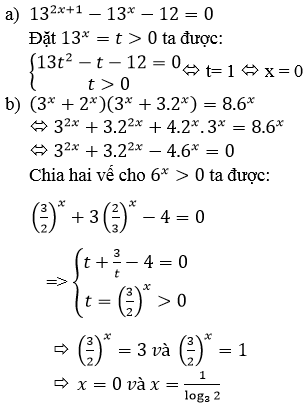
a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)