Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a, b thì Nguyễn Quang Duy làm đúng rồi.
c) \(a^{\dfrac{4}{3}}:\sqrt[3]{a}=a^{\dfrac{4}{3}}:a^{\dfrac{1}{3}}=a^{\dfrac{4}{3}-\dfrac{1}{3}}=a\)
d) \(\sqrt[3]{b}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}-\dfrac{1}{6}}=b^{\dfrac{1}{6}}\)

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

a) .
=
=
=
=
= 9.
b) :
=
=
=
=
=
= 8.
c) +
=
+
=
+
=
+
=
+
= 40.
d) -
=
-
=
-
=
-
= 121.
a) \(9^{\dfrac{2}{5}}.27^{\dfrac{2}{5}}=\left(9.27\right)^{\dfrac{2}{5}}=\left(3^2.3^3\right)^{\dfrac{2}{5}}=3^{5.\dfrac{2}{5}}=3^2=9\)
b) \(=\left(\dfrac{144}{9}\right)^{\dfrac{3}{4}}=\left(\dfrac{12}{3}\right)^{2.\dfrac{3}{4}}=4^{\dfrac{3}{2}}=2^{2.\dfrac{3}{2}}=2^3=8\)
c) \(=\left(\dfrac{1}{2}\right)^{4.\left(-0,75\right)}+\left(\dfrac{1}{4}\right)^{-\dfrac{5}{2}}\)
\(=\left(\dfrac{1}{2}\right)^{-3}+\left(\dfrac{1}{2}\right)^{-5}\)
\(=2^3+2^5=40\)
d) \(=\left(0,2\right)^{2.\left(-1.5\right)}-\left(0,5\right)^{3.\dfrac{-2}{3}}\)
\(=\left(\dfrac{1}{5}\right)^{-3}-\left(\dfrac{1}{2}\right)^{-2}\)
\(=5^3-2^2=121\)

a) ta có 2√5= = √20 ; 3√2 =
= √ 18 => 2√5 > 3√2
=> <
b) 6√3 = = √108 ; 3√6 =
= √54 => 6√3 > 3√6 =>
>
a) \(2\sqrt{5}=\sqrt{2^2.5}=\sqrt{20}\)
\(3\sqrt{2}=\sqrt{3^2.2}=\sqrt{18}\)
=> \(2\sqrt{5}>3\sqrt{2}\)
=> \(\left(\dfrac{1}{3}\right)^{2\sqrt{5}}< \left(\dfrac{1}{3}\right)^{3\sqrt{2}}\)
(vì cơ số \(\dfrac{1}{3}< 1\))
b) Vì \(3< 6^2\)
=> \(3^{\dfrac{1}{6}}< \left(6^2\right)^{\dfrac{1}{6}}\)
=> \(\sqrt[6]{3}< 6^{\dfrac{1}{3}}\)
=> \(\sqrt[6]{3}< \sqrt[3]{6}\)
=> \(7^{\sqrt[6]{3}}< 7^{\sqrt[3]{6}}\)

a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
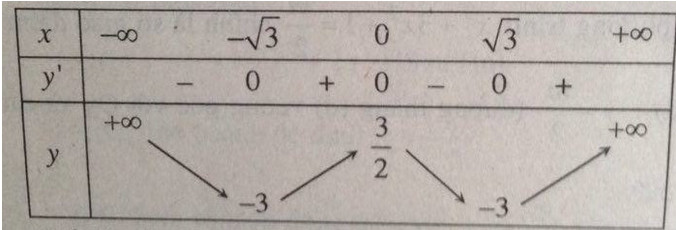
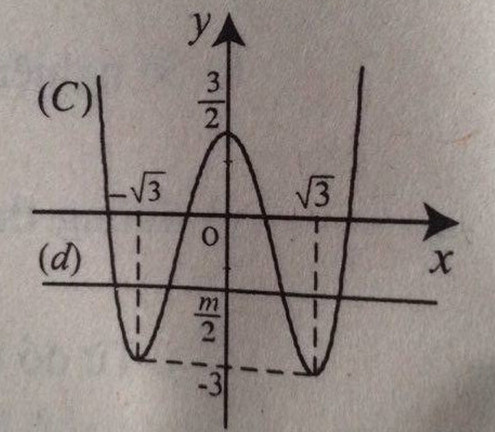
Đồ thị hàm số:
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm

a) Tập xác định : R\ {1}; y′=−4(x−1)2<0,∀x≠1y′=−4(x−1)2<0,∀x≠1 ;
Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.
Bảng biến thiên :
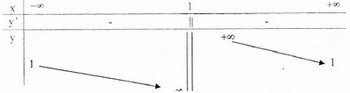
Đồ thị như hình bên. 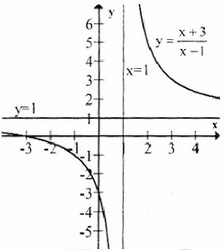
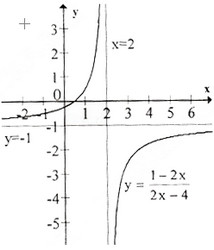
b) Tập xác định : R \{2}; y′=6(2x−4)2>0,∀x≠2y′=6(2x−4)2>0,∀x≠2
Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.
Bảng biến thiên :
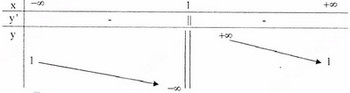
Đồ thị như hình bên.
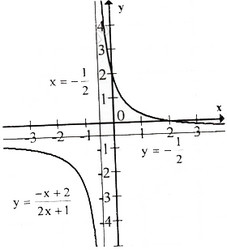
c) Tập xác định : R∖{−12}R∖{−12}; y′=−5(2x+1)2<0,∀x≠−12y′=−5(2x+1)2<0,∀x≠−12
Tiệm cận đứng : x=−12x=−12 . Tiệm cận ngang : y=−12y=−12.
Bảng biến thiên :
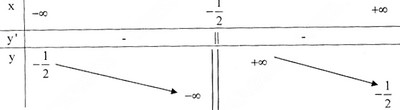
Đồ thị như hình bên.



a)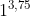 = 1 =
= 1 = 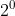 ;
; 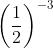 =
= 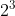 .
.
Mặt khác trong hai lũy thừa cungc cơ số lớn hơn 1, lũy thừa nào có số mũ lớn hơn là lũy thừa lớn hơn. Do đó theo thứ tự tăng dần ta được:
b)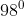 = 1 =
= 1 =  ;
; 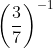 =
=  ;
; 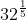 =
= 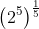 = 2 =
= 2 =  .
.
Do đó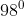 <
< 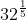 <
< 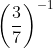 .
.