K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2022
a: \(=\left(2+\dfrac{4}{9}+4+\dfrac{5}{9}\right)+\left(-4-\dfrac{13}{21}-2-\dfrac{8}{21}\right)\)
=7-7
=0
b: \(=\dfrac{5}{23}\left(\dfrac{7}{13}+\dfrac{6}{13}\right)+\dfrac{18}{23}=\dfrac{5}{23}+\dfrac{18}{23}=1\)
c: \(=\dfrac{3}{7}\left(\dfrac{12}{19}-\dfrac{4}{19}\right)+\dfrac{4}{7}\cdot\dfrac{8}{19}\)
\(=\dfrac{3}{7}\cdot\dfrac{8}{19}+\dfrac{4}{7}\cdot\dfrac{8}{19}=\dfrac{8}{19}\)
d: \(=\dfrac{2}{5}+\dfrac{3}{5}:\dfrac{9-10}{15}-\dfrac{7}{2}\)
\(=\dfrac{-31}{10}+\dfrac{3}{5}\cdot\dfrac{-15}{1}=\dfrac{-31}{10}-9=\dfrac{-121}{10}\)
26 tháng 7 2023
a: x^3+8=(x+2)(x^2-2x+4)
b: =(3x+1)(9x^2-3x+1)
c: =(x+3)(x^2-3x+9)
d: =(4x-3y)(16x^2+24xy+9y^2)
MP
26 tháng 7 2023
\(a.x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
\(b.27x^3+1=\left(3x+1\right)\left(9x-3x+1\right)\)
\(c.x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)
\(d.64x^3-27y^3=\left(4x-3y\right)\left(16x^2+12xy+9y^2\right)\)
24 tháng 12 2023
Sửa đề: cắt DC tại M
a: Xét tứ giác ABMD có
AB//MD
AD//MB
Do đó: ABMD là hình bình hành
b: Ta có: ABMD là hình bình hành
=>AD=BM
mà AD=BC(ABCD là hình thang cân)
nên BM=BC
=>ΔBMC cân tại B
LT
4 tháng 6 2015
Ta có \(9=3^2\)hoặc\(9=9^1\)và\(343=7^3\)
Vì E và B là 2 số khác nhau nên \(E=9,A=1,D=7,B=3\)
Số C bằng:\(25-9-1-7-3=5\)
Đáp số :\(A=1,B=3,C=5,D=7,E=9\)
KC
1
25 tháng 6 2015
Thay p = e vào p + e = 2n ta có
p +p = 2n => 2p = 2n => p = n
Vì p = n
=> p + n = 40 => p + p = 40 => p = 20
=> p = n = e = 20
Vậy p = n = e = 20
11 tháng 8 2018
a) \(E=\left(\frac{1}{x+2}+\frac{1}{x-2}\right).\frac{x-2}{x}\left(ĐKXĐ:x\ne0;x\ne\pm2\right)\)
\(=\left(\frac{x-2+x+2}{\left(x+2\right)\left(x-2\right)}\right).\frac{x-2}{x}\)
\(=\frac{2x}{\left(x-2\right)\left(x+2\right)}.\frac{x-2}{x}=\frac{2x\left(x-2\right)}{x\left(x-2\right)\left(x+2\right)}=\frac{2}{x+2}\)
b) Khi x = 6 \(\Rightarrow E=\frac{2}{x+2}=\frac{2}{6+2}=\frac{2}{8}=\frac{1}{4}\)
c) \(E=4\Leftrightarrow\frac{2}{x+2}=4\Leftrightarrow4\left(x+2\right)=2\Leftrightarrow4x+8=2\Leftrightarrow x=\frac{-3}{2}\)
Vậy để E = 4 thì x = -3/2
d) \(E>0\Leftrightarrow\frac{2}{x+2}>0\Leftrightarrow2>0\)
Vậy phương trình vô nghiệm
e) \(E\in Z\Leftrightarrow x+2\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
Nếu x + 2 = 1 thì x = -1
Nếu x + 2 = -1 thì x = -3
Nếu x + 2 = 2 thì x = 0
Nếu x + 2 = -2 thì x = -4
Vậy ...
LP
11 tháng 8 2018
Nek bạn giải thích hộ mik tí nữa nhé :Tại sao 2 > 0 thì phương trình lại vô nghiệm ?
8 tháng 4 2021
a, \(E=\left(\frac{x^2+4}{x^2-4}+\frac{6}{6-3x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)ĐK : \(x\ne\pm2\)
\(=\left(\frac{x^2+4}{x^2-4}+\frac{2}{2-x}+\frac{1}{x+2}\right):\left(\frac{x^2-4+10-x^2}{x+2}\right)\)
\(=\left(\frac{x^2+4-2\left(x+2\right)+x-2}{\left(x-2\right)\left(x+2\right)}\right):\left(\frac{6}{x+2}\right)\)
\(=\frac{x^2+4-2x-4+x-2}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{6}=\frac{x^2-x-2}{6\left(x-2\right)}=\frac{x+1}{6}\)
b, Ta có : \(\left|2x-3\right|=1\Leftrightarrow\orbr{\begin{cases}2x-3=1\\2x-3=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\left(ktmđk\right)\\x=1\end{cases}}}\)
Thay x = 1 vào biểu thức E ta được : \(\frac{1+1}{6}=\frac{2}{6}=\frac{1}{3}\)
Vậy với x = 1 thì E = 1/3
c, Ta có : \(E< 0\)hay \(\frac{x+1}{6}< 0\Rightarrow x+1>0\)( do 6 > 0 )
\(\Leftrightarrow x>-1\)
Với với x > -1 thì E < 0
d, Ta có E = 3 - x hay \(\frac{x+1}{6}=3-x\Rightarrow x+1=18-6x\Leftrightarrow7x=17\Leftrightarrow x=\frac{17}{7}\)
TM
2 tháng 3 2017
Áp dụng bất đẳng thức Nesbitt với 3 số dương d,e,f ta có: \(\frac{d}{e+f}+\frac{e}{d+f}+\frac{f}{d+e}\ge\frac{3}{2}\)
Dấu "=" xảy ra khi d=e=f
2 tháng 3 2017
Chứng minh rằng \(\frac{d}{e+f}+\frac{e}{d+f}+\frac{f}{d+e}\ge\frac{3}{2}\)\(\forall d,e,f>0\)
\(\Rightarrow\frac{d}{e+f}+1+\frac{e}{d+f}+1+\frac{f}{d+e}+1\ge\frac{9}{2}\)
\(\Rightarrow\frac{d+e+f}{e+f}+\frac{d+e+f}{d+f}+\frac{d+e+f}{d+e}\ge\frac{9}{2}\)
\(\Rightarrow\left(d+e+f\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge\frac{9}{2}\)
\(\Rightarrow2\left(d+e+f\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge9\)
\(\Rightarrow\left(e+f+d+f+d+e\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge9\)
Áp dụng bất đẳng thức Cauchy
\(\Rightarrow\left(e+f+d+f+d+e\right)\left(\frac{1}{e+f}+\frac{1}{d+f}+\frac{1}{d+e}\right)\ge9\sqrt[3]{\left(e+f\right)\left(d+f\right)\left(d+e\right).\frac{1}{\left(e+f\right)\left(d+f\right)\left(d+e\right)}}=9\)
Vậy ta có đpcm
Dấu " = " xảy ra khi \(e=d=f\) ( đpcm )
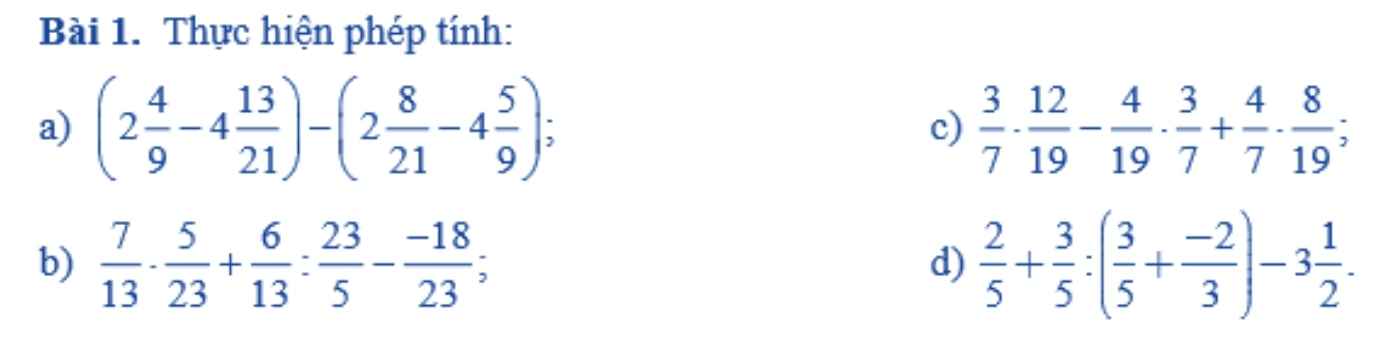
a có thấy gì đâu mag giúp