Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số thứ nhất là \(x\) (\(x\) \(\in\) N)
Thì số thứ hai là: \(x\) + 1
Số thứ ba là: \(x\) + 2
Theo bài ra ta có: \(x\) + (\(x\) + 1) + (\(x\) + 2) = 2256
\(x\) + \(x\) + 1 + \(x\) + 2 = 2256
3\(x\) + 3 = 2256
3\(x\) = 2256 - 3
3\(x\) = 2253
\(x\) = 2253 : 3
\(x\) = 751
Vậy số nhỏ nhất cần tìm là 751

Lời giải:
Gọi ba số tự nhiên liên tiếp là $a,a+1, a+2$. Tổng của chúng là:
$a+(a+1)+(a+2)=1194$
$a+a+a+1+2=1194$
$a\times 3+3=1194$
$a\times 3=1194-3=1191$
$a=1191:3=397$
Số lớn nhất trong 3 số: $397+2=399$
- Gọi số đầu tiên trong dãy các số tự nhiên liên tiếp là: x
Ta có:
x + (x + 1) + (x + 2) = 1194
x . 3 + (1 + 2) = 1194
x . 3 + 3 = 1194
x . 3 = 1194 - 3
x . 3 = 1191
x = 1191 : 3
x = 397
=> Số lớn nhất trong dãy ba số tự nhiên liên tiếp là: (x + 2)
=> Số đó là: 397 + 2 = 399
Vậy số đó là 399

Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
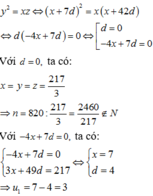
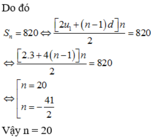


Gọi 2n là số tự nhiên chẵn thứ nhất (\(n\in |N\))
Ta có, 4 số tự nhiên chẵn liên tiếp là: 2n; 2n+2; 2n+4; 2n+6
Theo đề, ta có: 2n + 2n+2 + 2n+4 + 2n+6 =5420
<=> 4.2n + 12 = 5420
<=> 2n = (5420 - 12)/4
<=> 2n = 1352 (nhận, vì 2n \(\in\) N nên n \(\in\) N)
Vậy 4 số tự nhiên chẵn liên tiếp là: 1352; 1354; 1356; 1358

gọi số đó là abc(a,b,c là các số khác nhau)
=>abc=ab+bc+ca+ba+cb+ac
=>abc=a0+b+b0+c+c0+a+b0+a+c0+b+a0+c
=>abc=2aa+2bb+2cc
=>78a=12b+21c<12.9+21.9=297
=>a<4=>a=1;2;3
vì abc lớn nhất nên ta chọn a=3=>12b+21c=234
=>4b+7c=78
chọn b lớn nhất có thể : thử b=9=>c=6(nhận)
vậy số lớn nhất đó là 396
Trung bình cộng của ba số tự nhiên liên tiếp bằng số thứ hai và bằng:
2256 : 3 = 752
Số thứ nhất là: 752 - 1 = 751
Đáp số: 751
ccc