Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Số cần lập là a b c d e f ¯ , ta có a + b + c − 1 = d + e + f ⇔ 20 = 2 d + e + f ⇔ d + e + f = 10
Với mỗi f ∈ 1 ; 3 ; 5 ⇒ d , e có 4 cách chọn, suy ra a b c d e f ¯ có 4.3 ! = 24 cách chọn
Suy ra có 3.24 = 72 số có thể lập thỏa mãn đề bài

gọi số đó là \(\overline{abcd}\) ở đó a,b,c,d thuộc {1,2,5,7}
a, để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng chữ số 5 hoặc 7.
vậy chữ số a có 2 cách chọn, chữ số b có 4 cách chọn
chữ số c có 4 cách chọn, d cũng có 4 cách chọn
suy ra có tất cả các chữ số ớn hơn 4000 là 2.4.4.4=128 số
b, để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng 5 hoặc 7
mà các chữ số khác nhau
suy ra b có 3 cách chọn, c có 2 cách chọn và d có 1 cách chọn
số các chữ số cần tìm là: 2.3.2.1=12 số

Đáp án A
Tập 1 ; 2 ; 3 ; 4 ; 5 ; 6 có 6 số và tạo thành có 5 vị trí. Mỗi số có 5 chữ số tạo thành một chỉnh hợp chập 5 của 6 chữ số trên A 6 5 = 720
Trong 720 số đó mỗi vị trí (hàng chục nghìn, nghìn, trăm, chục, đơn vị) mỗi chữ số 1, 2, 3, 4, 5, 6 có mặt 720 6 = 120 lần. Tổng các chữ số 1 + 2 + 3 + 4 + 5 + 6 = 21 .
Vậy tổng của 720 số tạo thành là 120.21.11111 = 27999720

Đáp án D
Số cách sắp xếp 5 chữ số khác nhau là: A 9 5
Giữa 5 số đó có 6 chỗ trống nhưng số 0 không thể đứng đầu nên số cách sắp xếp 3 chữ số 0 là: C 5 3 = 10 cách
Vậy số các số gồm 8 chữ số thỏa mãn yêu cầu đề bài là: A 9 5 .10 = 151200

Gọi số cần tìm có dạng a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 ¯
+) Chọn vị trí của 3 chữ số 0 trong 7 vị trí (trừ a 1 ). Vì giữa 2 chữ số 0 luôn ít nhất 1 chữ số khác 0 nên chọn 3 vị trí trong 5 vị trí để điền các số 0, sau đó thêm vào giữa 2 số 0 gần nhau 1 vị trí nữa.
Suy ra số cách chọn là C 5 3 = 10
+) Chọn các số còn lại, ta chọn bộ 5 chữ số trong 9 chữ số từ 1 đến 9, có A 9 5 cách chọn.
Vậy có tất cả 10 . A 9 5 = 151200 số cần tìm.
Chọn đáp án D.

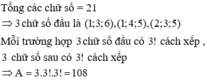


gọi số đó là abc(a,b,c là các số khác nhau)
=>abc=ab+bc+ca+ba+cb+ac
=>abc=a0+b+b0+c+c0+a+b0+a+c0+b+a0+c
=>abc=2aa+2bb+2cc
=>78a=12b+21c<12.9+21.9=297
=>a<4=>a=1;2;3
vì abc lớn nhất nên ta chọn a=3=>12b+21c=234
=>4b+7c=78
chọn b lớn nhất có thể : thử b=9=>c=6(nhận)
vậy số lớn nhất đó là 396