K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 7 2023
`a, (x-y)^2 = (x+y)^2 - 4xy = 12^2 - 35 . 4 = 144 - 140 = 4`.
`b, (x+y)^2 = (x-y)^2 + 4xy = 8^2 + 20.4 = 64 + 80 = 144`
`c, x^3 + y^3 = (x+y)^3 - 3xy(x+y) = 5^3 - 3 . 6 . 5 = 125 - 90 = 35`
`d, x^3 - y^3 = (x-y)^3 - 3xy(x-y) = 3^3 - 3 .40 . 3 = 27 - 360 = -333`.
8 tháng 8 2017
(x+y)^2 =a^2
x^2 +2xy +y^2 =a^2
x^2+y^2 =a^2-2xy =a^2 -2b
x^3 +y^3 = (x+y)(x^2 -xy +y^2)
=a(a^2-2b-b)
=a(a^2-3b)
=a^3- 3ab
(x^2 +y^2)^2=(a^2-2b)^2 ( cái này tính cho x^4 + y^4)
tương tự như câu đầu tiên
x^5+ y^5 (cái đó mình không biết)
CG
1
NM
Nguyễn Minh Quang
Giáo viên
12 tháng 8 2021
a. ta có : \(x^2+y^2=\left(x+y\right)^2-2xy=1^2-2\times\left(-6\right)=13\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=1^3-3\times\left(-6\right)\times1=19\)
\(x^5+y^5=\left(x+y\right)\left[x^4-x^3y+x^2y^2-xy^3+y^4\right]\)
\(=\left(x+y\right)\left[\left(x^2+y^2\right)^2-x^2y^2-xy\left(x^2+y^2\right)\right]=1.\left(13^2-\left(-6\right)^2-\left(-6\right).13\right)=211\)
b.\(x^2+y^2=\left(x-y\right)^2+2xy=1+2\times6=13\)
\(x^3-y^3=\left(x-y\right)^3+3xy\left(x-y\right)=1^3+6.3.1=19\)
\(x^5-y^5=\left(x-y\right)\left[\left(x^4+x^3y+x^2y^2+xy^3+y^4\right)\right]\)
\(=\left(x-y\right)\left[\left(x^2+y^2\right)^2-x^2y^2+xy\left(x^2+y^2\right)\right]=1.\left(13^2-6^2+6.13\right)=211\)
VD
2
2 tháng 1 2017
\(\frac{\left(x^2+xy+y^2\right)\left(x^2-xy+y^2\right)}{\left(x^3+y^3\right)\left(x^3-y^3\right)}=\frac{1}{x^2-y^2}\)
2 tháng 1 2017
Có bạn giúp rồi nhé. M khỏi làm nữa nhé. Bài của bạn ngonhuminh là dùng hằng đẳng thức không đó b.
17 tháng 8 2021
a: \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(=3^3-3\cdot3\cdot\left(-2\right)\)
\(=27+18=45\)
b: \(\left(x^3+y^3\right)^2=45^2=2025\)
VD
2
TM
2 tháng 1 2017
\(\frac{\frac{x^2+xy+y^2}{x^3+y^3}}{\frac{x^3-y^3}{x^2-xy+y^2}}=\frac{x^2+xy+y^2}{x^3+y^3}.\frac{x^2-xy+y^2}{x^3-y^3}=\frac{x^2+xy+y^2}{\left(x+y\right)\left(x^2-xy+y^2\right)}.\frac{x^2-xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\frac{1}{\left(x+y\right)\left(x-y\right)}=\frac{1}{x^2-y^2}\)
TK
2
AM
28 tháng 6 2015
x+y=7
=>(x+y)3-3xy(x+y)=73-3.10.7
<=>x3+3x2y+3xy2+y3-3x2y-3xy2=133
<=>x3+y3=133
=>(x-y)3+3xy(x-y)
=x3-3x2y+3xy2-y3+3x2y-3xy2
=x3-y3
*)Với x-y=3=>x3-y3=(x-y)3+3xy(x-y)=33+3.10.3=117
*))Với x-y=3=>x3-y3=(x-y)3+3xy(x-y)=(-3)3+3.10.(-3)=-117
28 tháng 6 2015
x + y = 7 => x = 7 - y thay vào x.y ta có:
( 7 -y) y = 10 =>7y - y^2 = 10 => y^2 - 7y + 10 = 0 => y^2 -2y - 5y +10 => y( y-2) - 5 (y - 2) = 0
=> ( y - 5)(y - 2) = 0 => y = 5 hoặc 2 => x = 2 hoặc 5 ( Nếu bạn thêm đk x > y hay y>x chior có một trường hợp thôi)
(+) y = 5 và x = 2
=> x - y = 2- 5 = -5
x^2 + y^2 = 2^2 + 5^2 = 4 + 25 = 29
x^3 + y^3 = 2^3 + 5^3 = 8 + 125 = 133
x^3 - y^3 = 2^3 - 5^3 = 8 -125 = -117
(+) Tương tự x = 5 và y = 2
25 tháng 6 2017
x2+y2=x2+2xy+y2-2xy =(x+y)2-2xy =22-2.3 =4-3 =1
x3+y3=x3+3x2y+3xy2+y3-3x2y-3xy2 =(x+y)3-3xy(x+y) =23-3.3.2 =-10
câu còn lại tương tự nhé
H
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 8 2023
1/
\(x^2+y^2=\left(x-y\right)^2+2xy=2^2+2.1=6\)
2/
\(x^3-y^3=\left(x-y\right)\left(x^2+y^2+xy\right)=2\left(6+1\right)=14\)
3/
\(x^2-y^2=\left(x-y\right)\left(x+y\right)=2\left(x+y\right)\) (3)
Ta có
\(x^2+y^2=\left(x+y\right)^2-2xy=\left(x+y\right)^2-2=6\)
\(\Rightarrow\left(x+y\right)^2=8\Rightarrow\left(x+y\right)=\pm2\sqrt{2}\) Thay vào (3)
\(\Rightarrow x^2-y^2=2.\pm2\sqrt{2}=\pm4\sqrt{2}\)
4/
\(x^6-y^6=\left(x^3-y^3\right)\left(x^3+y^3\right)\) (4)
Ta có
\(x^3-y^3=14\) (cmt)
Ta có
\(x^3+y^3=\left(x+y\right)\left(x^2+y^2-xy\right)=\left(x+y\right).5=\pm2\sqrt{2}.5=\pm10\sqrt{2}\)
\(\Rightarrow x^6-y^6=\pm10\sqrt{2}.14=\pm140\sqrt{2}\)
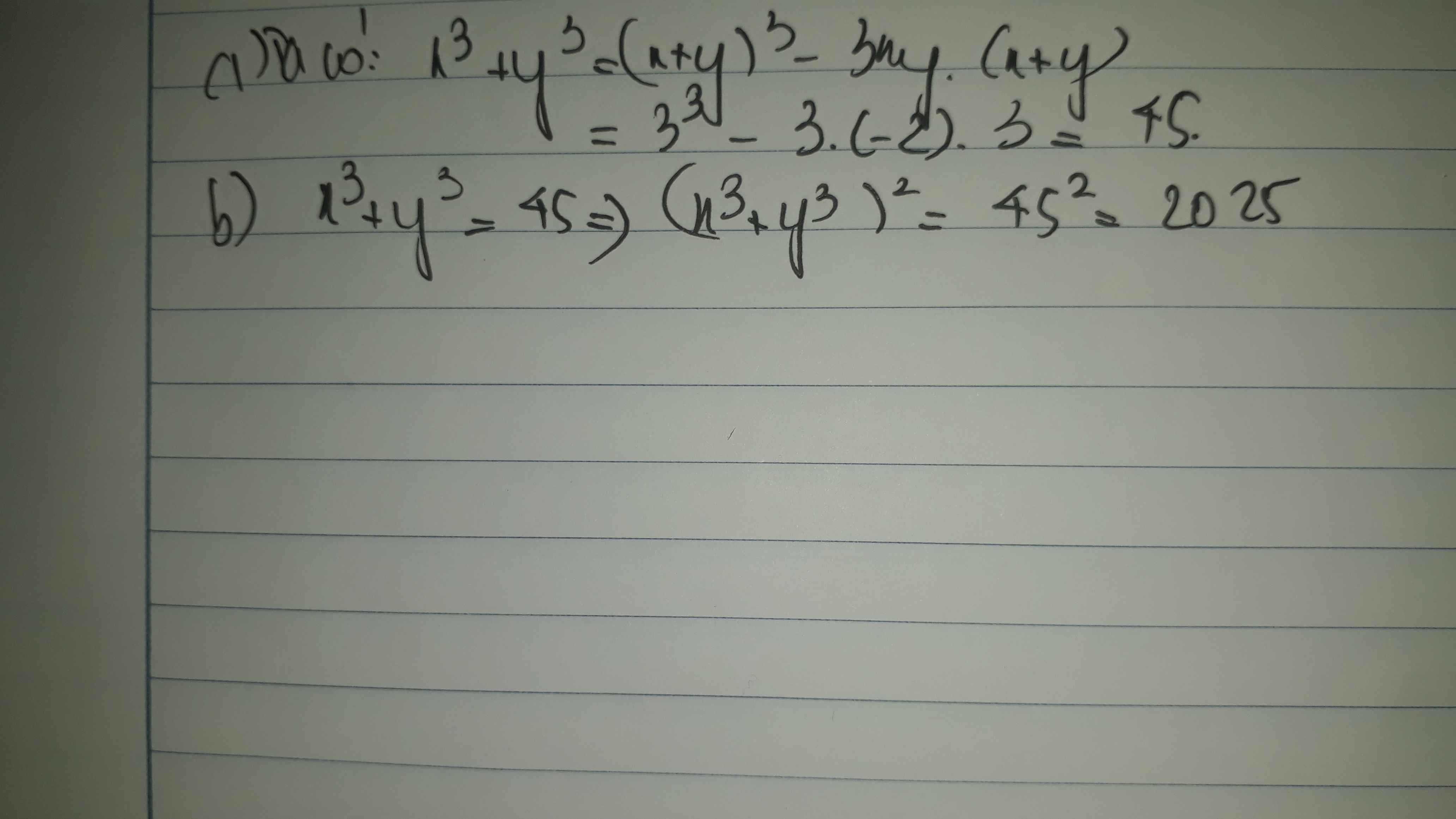
Ta có: \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
Thay \(x+y=2\)và \(xy=-2\)vào biểu thức ta được:
\(x^3+y^3=2^3-3.\left(-2\right).2=20\)
x3 + y3 = x3 + 3x2y + 3xy2 + y3 - 3x2y - 3xy2
= ( x3 + 3x2y + 3xy2 + y3 ) - ( 3x2y + 3xy2 )
= ( x + y )3 - 3xy( x + y )
= 23 - 3.(-2).2
= 8 + 12 = 20