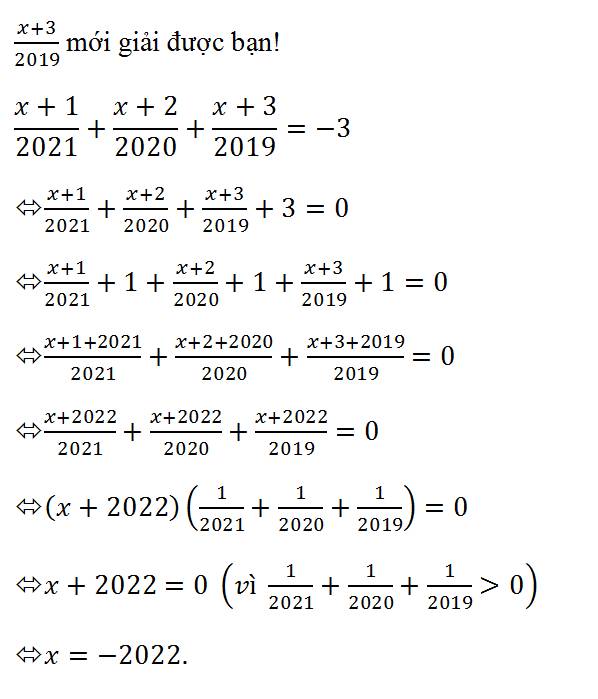K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PN
0
1 tháng 6 2019
\(A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2019.2020}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2019}-\frac{1}{2020}\)
\(A=1-\frac{1}{2020}\)
\(A=\frac{2019}{2020}\)
1 tháng 6 2019
\(B=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{2017.2019}\)
\(2B=\frac{2}{1.3}+\frac{2}{3.5}=\frac{2}{5.7}+...+\frac{2}{2017.2019}\)
\(2B=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}=\frac{1}{5}-\frac{1}{7}+...+\frac{1}{2017}-\frac{1}{2019}\)
\(2B=1-\frac{1}{2019}\)
\(2B=\frac{2018}{2019}\)
\(B=\frac{2018}{2019}:2=\frac{1009}{2019}\)
F
Tim x biet
\(\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{2}{x\left(x+1\right)}=\frac{2019}{2020}\)
1
7 tháng 6 2020
\(\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{2}{x\left(x+1\right)}=\frac{2019}{2020}\)
=> \(\frac{2}{6}+\frac{2}{12}+\frac{2}{20}+...+\frac{2}{x\left(x+1\right)}=\frac{2019}{2020}\)
=> \(2\left(\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{x\left(x+1\right)}\right)=\frac{2019}{2020}\)
=> \(2\left(\frac{1}{2}-\frac{1}{x+1}\right)=\frac{2019}{2020}\)
=> \(1-\frac{2}{x+1}=\frac{2019}{2020}\)
=> \(\frac{2}{x+1}=\frac{1}{2020}=\frac{2}{4040}\)
=> x + 1 = 4040 => x = 4039
10 tháng 3 2019
Ta có x+1/2018 + x+1/2019 + x+1/2020 = 0
=> (x+1).(1/2018 + 1/2019+ 1/2020) = 0
Vì 1/2018 + 1/2019 + 1/2020 > 0
=> x+1 = 0
=> x = -1
DL
1
21 tháng 2 2020
x + (x + 1) + (x + 2) + (x + 3) + ..... + 2019 + 2020 = 2020
Ta gọi biểu thức đấy là B
x + (x + 1) + (x + 2) + (x + 3) + ..... + 2019 = 2020 - 2020
x + (x + 1) + (x + 2) + (x + 3) + ..... + 2019 = 0
Có 2020 - x số hạng
B = \(\frac{\text{(2019 − x)(2020 - x)}}{\text{2}}=0\)
=> 2019 + x = 0
x = -2019
=> 2020 - x = 0
x = 2020
➤ Vậy x = {-2019; 2020}
2 tháng 8 2019
a) (x - 1)3 - 1 = 0
<=> (x - 1)3 = 0 + 1
<=> (x - 1)3 = 1
<=> (x - 1)3 = 13
<=> x - 1 = 1
<=> x = 1 + 1
<=> x = 2
=> x = 2
b) (x - 4)2019 = 1
<=> (x - 4)2019 = 12019
<=> x - 4 = 1
<=> x = 1 + 4
<=> x = 5
=> x = 5
c) (x - 2019)2020 = 0
<=> (x - 2019)2020 = 02020
<=> x - 2019 = 0
<=> x = 0 + 2019
<=> x = 2019
=> x = 2019
d) (x - 1)2 = (x - 1)3
<=> x2 - 2x + 1 = x3 - 2x2 + x - x2 + 2x - 1
<=> x2 - 2x + 1 = x3 - 3x2 + 3 - 1
<=> x2 - 2x + 1 - x3 + 3x2 - 3 + 1 = 0
<=> 4x2 - 5x + 2 - x3 = 0
<=> (-x2 + 3x - 2)(x - 1) = 0
<=> (x2 - 3x + 2)(x - 1) = 0
<=> (x - 2)(x - 1)(x - 1) = 0
<=> x - 2 = 0 hoặc x - 1 = 0
x = 0 + 2 x = 0 + 1
x = 2 x = 1
=> x = 1 hoặc x = 2
NH
1
