Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\sqrt{x^2-x+1}\)
\(=\sqrt{x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}}\)
\(=\sqrt{\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\)
Mà: \(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\)
Nên bt luôn có nghĩa
b) \(\dfrac{5}{\sqrt{1-\sqrt{x-1}}}\) có nghĩa khi:
\(\left\{{}\begin{matrix}x-1\ge0\\1-\sqrt{x-1}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x-1< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1\le x\\x< 2\end{matrix}\right.\Leftrightarrow1\le x< 2\)
c) \(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\) có nghĩa khi:
\(x\ge0\)
d) \(\dfrac{\sqrt{-3x}}{x^2-1}\) có nghĩa khi:
\(\Leftrightarrow\left\{{}\begin{matrix}-3x\ge0\\x^2-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le0\\x\ne\pm1\end{matrix}\right.\)
e) \(\dfrac{2}{\sqrt{x}-2}\) có nghĩa khi:
\(\left\{{}\begin{matrix}x\ge0\\\sqrt{x}-2\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)

Ta có: x 2 +2 + 2 2 = 2(1 + 2 )x ⇔ x 2 - 2(1+ 2 )x +2 +2 2 = 0
∆ ' = b ' 2 – ac = - 1 + 2 2 - 1(2+2 2 )
= 1 + 2 2 +2 -2 -2 2 =1 > 0
∆ ' = 1 =1
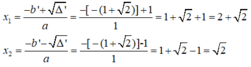
Vậy với x= 2+ 2 hoặc x = 2 thì giá trị của hai biểu thức trên bằng nhau
Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau? -2 2 x – 1 và 2 x 2 + 2x +3

Ta có: -2 2 x – 1 = 2 x 2 + 2x +3 ⇔ 2 x 2 +2x + 3 + 2 2 x + 1=0
⇔ 2 x 2 + 2(1 + 2 )x +4 =0
∆ ' = b ' 2 – ac= 1 + 2 2 - √2 .4= 1+2 2 +2 - 4 2
= 1-2 2 +2 = 2 - 1 2 > 0
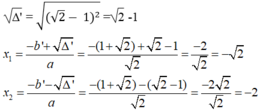
Vậy với x= - 2 hoặc x = -2 thì giá trị của hai biểu thức trên bằng nhau

Ta có: 3 x 2 + 2 5 x - 3 3 = - x 2 - 2 3 x +2 5 +1
⇔ 3 x 2 + 2 5 x - 3 3 + x 2 + 2 3 x - 2 5 – 1= 0
⇔ ( 3 +1) x 2 + (2 5 + 2 3 )x -3 3 - 2 5 – 1= 0
⇔ ( 3 +1)x2 + 2( 5 + 3 )x -3 3 - 2 5 – 1= 0
∆ ' = b ' 2 – ac= 3 + 5 2 – ( 3 + 1 )( -3 3 - 2 5 – 1)
= 5 + 2 15 +3+9 +2 15 + 3 +3 3 +2 5 + 1
=18 +4 15 +4 3 +2 5
= 1 + 12 + 5 + 2.2 3 + 2 5 + 2.2 3 . 5
= 1 + 2 3 2 + 5 2 + 2.1.2 3 +2.1. 5 + 2.2 5 . 3
= 1 + 2 3 + 5 2 > 0
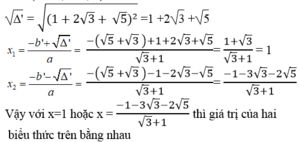
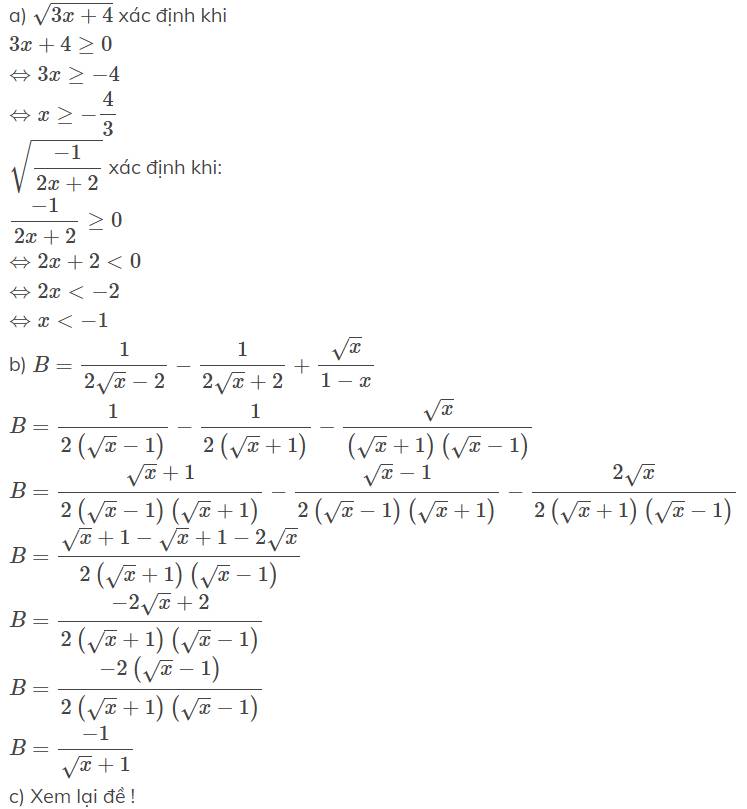

 (Với x > 0; x 1; x4)
(Với x > 0; x 1; x4)
Biểu thức có nghĩa khi và chỉ khi:
x - 2 ≠ 0 x - 2 ≥ 0 ⇔ x ≠ 2 x ≥ 2 ⇔ x > 2