Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có: \(OM\perp QS\) => \(\widehat{QMO}=90^o\)
\(OB\perp PB\) (vì PB là tiếp tuyến của đường tròn tâm O) => \(\widehat{OBP}=90^o\)
tứ giác OBQM có: \(\widehat{OBQ}+\widehat{OMQ}=180^o\)
mà 2 góc này ở vị trí đối nhau
=> tứ giác OBQM nội tiếp đường tròn
=> \(\widehat{OBM}=\widehat{OQM}\) (vì cùng chắn cung OM nhỏ)(1)
ta lại có: tam giác OAB cân tại O (vì OA=OB=R)
=> \(\widehat{OAB}=\widehat{OBA}\left(2\right)\)
Ta có: \(OA\perp PA\) (vì PA là tiếp tuyến của đường tròn tâm O)
=> \(\widehat{OAP}=90^o\) mà góc OAP +góc OAS =180o(2 góc kề bù)
=> góc OAS =90o
tứ giác OMAS có: \(\widehat{OAS}=\widehat{OMS}\left(=90^o\right)\)
mà 2 goc snày ở vị trí kề nhua cùng nhìn cạnh OS
=> tứ giác OMAS nội tiếp
=> góc OAM = góc OMS(3)
từ (1); (2) và(3) ta có: góc OQM = góc OSM
=> Tam giác OQS cân tại O
=> đường cao OM đồng thời là đường trung tuyến
=> M là trung điểm của QS
hay MQ =MS(ĐPCM)

a: Xét tứ giác OBMA có \(\widehat{OBM}+\widehat{OAM}=90^0+90^0=180^0\)
nên OBMA là tứ giác nội tiếp
=>O,B,M,A cùng thuộc một đường tròn
b: Ta có: ΔOBC cân tại O
mà OM là đường cao
nên OM là phân giác của góc BOC
Xét ΔOBM và ΔOCM có
OB=OC
\(\widehat{BOM}=\widehat{COM}\)
OM chung
Do đó: ΔOBM=ΔOCM
=>\(\widehat{OBM}=\widehat{OCM}\)
mà \(\widehat{OBM}=90^0\)
nên \(\widehat{OCM}=90^0\)
=>MC là tiếp tuyến của (O)
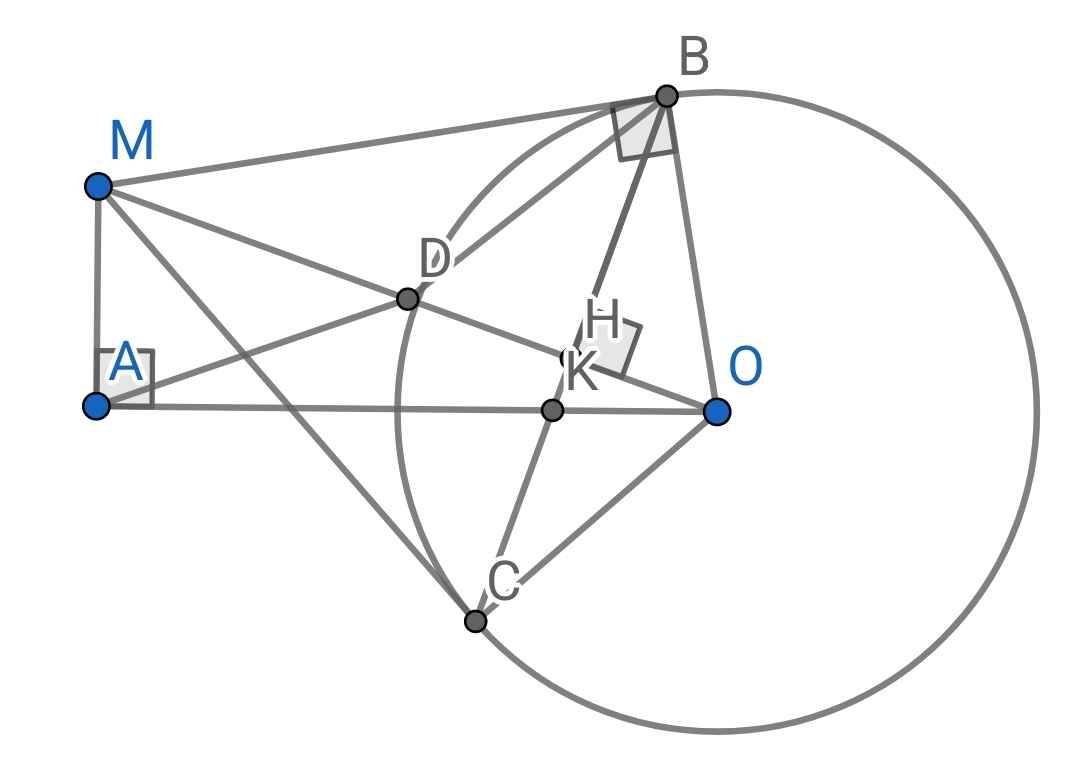 a) Gọi D là trung điểm của MO
a) Gọi D là trung điểm của MO
∆OAM vuông tại A có AD là đường trung tuyến ứng với cạnh huyền OM
⇒ AD = OD = MD = OM : 2 (1)
∆OBM vuông tại B có BD là đường trung tuyến ứng với cạnh huyền OM
⇒ BD = OD = MD = OM : 2 (2)
Từ (1) và (2) ⇒ AD = BD = OD = MD
Vậy A, B, O, M cùng thuộc (D, AD)
b) Xét hai tam giác vuông: ∆OHB và ∆OHC có:
OH là cạnh chung
OB = OC = bán kính
⇒ ∆OHB = ∆OHC (cạnh huyền - cạnh góc vuông)
⇒ ∠HOB = ∠HOC (hai góc tương ứng)
⇒ ∠MOB = ∠MOC
Xét ∆MOB và ∆MOC có:
OM là cạnh chung
∠MOB = ∠MOC (cmt)
OB = OC = bán kính)
⇒ ∆MOB = ∆MOC (c-g-c)
⇒ ∠OBM = ∠OCM (hai góc tương ứng)
⇒ ∠OCM = 90⁰
⇒ MC ⊥ OC
Mà OC là bán kính của (O)
⇒ MC là tiếp tuyến của (O)

a ) Ta có : PA // BC => ^MPE = ^ECB = ^PBM vì PB là tiếp tuyến của (O)
=> \(\Delta MPE~\Delta MBP\left(g.g\right)\)
\(\Rightarrow\frac{MP}{MB}=\frac{ME}{MP}\Rightarrow MP^2=ME.MB\)
b ) .Ta có MA là tiếp tuyến của (O)
\(\Rightarrow\widehat{MAE}=\widehat{MBA}\Rightarrow\Delta MAE~\Delta MBA\left(g.g\right)\)
\(\Rightarrow\frac{MA}{MB}=\frac{ME}{MA}\Rightarrow MA^2=ME.MB\)
\(\Rightarrow MA^2=MP^2\Rightarrow MA=MP\Rightarrow M\) là trung điểm PA