K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 12 2021
\(a,=\dfrac{2y}{x}\\ b,=\dfrac{3\left(x+4\right)}{4\left(x-4\right)}\cdot\dfrac{-2\left(x-4\right)}{x+4}=\dfrac{-3}{2}\\ c,=\dfrac{\left(x+2\right)^2}{2\left(x-3\right)}\cdot\dfrac{x-3}{x+2}=\dfrac{x+2}{2}\\ d,=\dfrac{x+4+2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{3x}{x^2-4}\)
L
26 tháng 12 2021
a, \(\dfrac{2y}{x}\)
b, \(\dfrac{3\left(x+4\right)}{4\left(x-4\right)}.\dfrac{-2\left(x-4\right)}{x+4}=\dfrac{-3}{2}\)
c, \(\dfrac{\left(x+2\right)^2}{2\left(x-3\right)}.\dfrac{x-3}{x+2}=\dfrac{x+2}{2}\)
d, \(\dfrac{x+4}{\left(x-2\right)\left(x+2\right)}+\dfrac{2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{x+4+2x-4}{\left(x+2\right)\left(x-2\right)}=\dfrac{3x}{x^2-4}\)
MK
1
21 tháng 7 2017
\(x^3+x=0\)
\(\Leftrightarrow x\left(x^2+1\right)=0\)
thấy :x2+1>0 loại
suy ra x=0
NA
2
29 tháng 9 2018
Có 25t\(^2\) - 260t + 1700
= ( 5t )\(^2\) - 2 . 5t . 26 + 26\(^2\) + 1024
= ( 5t - 26 ) \(^2\) + 1024
\(\Rightarrow\) x\(^2\) = ( 5t - 26 ) \(^2\) + 1024
Có ( 5t - 26 )\(^2\) \(\ge\) 0 với mọi t
\(\Rightarrow\) ( 5t - 26 ) \(^2\) + 1024 \(\ge\) 1024 với mọi t
Dấu " = " xảy ra \(\Leftrightarrow\) ( 5t - 26 )\(^2\) = 0
\(\Rightarrow\) t = \(\frac{26}{5}\)
Vậy x\(^2\) đạt GTNN là 1024 khi t = \(\frac{26}{5}\)
29 tháng 9 2018
\(x^2=25t^2-260t+1700\)
\(x^2=\left(5t\right)^2-2\cdot5t\cdot26+26^2+1024\)
\(x^2=\left(5t-26\right)^2+1024\)
Vì \(\left(5t-26\right)^2\ge0\forall t\)
\(\Rightarrow x^2\ge1024\forall t\)
Dấu "=" xảy ra \(\Leftrightarrow5t-26=0\Leftrightarrow t=\frac{26}{5}\)
Vậy x2min = 1024 <=> t = 26/5
25 tháng 11 2018
Cái gì có khối lượng thì sẽ tạo ra một áp suất đè nên những vật ở dưới nó
29 tháng 9 2019
Lớp 8 nên sử dụng hằng đẳng thức
(=) X3 +3x2 +y3+5y2-x3-y3=0
(
24 tháng 6 2019
Ta có
\(\left(1+\sqrt{15}\right)^2=16+2\sqrt{15}< 16+2\sqrt{16}=16+8=24\)
Ta lại có \(\sqrt{24}^2=24\)
Vậy \(1+\sqrt{15}< \sqrt{24}\)
24 tháng 6 2019
Bài làm
Ta có: ( 1 + V15 )2 = 1 + 15 + 2 V15 = 16 + 2V15
V24 2 = 24 = 16 + 8
Vì V152 = 15 < 16 = 42
Nên V15 < 4
=> 2V15 < 8
=> 16 + 2V15 < 24
=> ( 1 + V15 )2 < V24 2
Vậy 1 + V15 < V24
# Chúc bạn học tốt #
ST
29 tháng 3 2018
\(a+b+c=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)=0
\(\Leftrightarrow\)\(a^3+ab^2+ac^2-a^2b-a^2c-abc+a^2b+b^3+bc^2-ab^2-\)
\(abc-b^2c+ca^2+bc^2+c^3-abc-ac^2-bc^2\)=0
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\Leftrightarrow a^3+b^3-3abc=-c^3\)
TN
2
TT
15 tháng 12 2017
\(5x\left(x-1\right)-3\left(1-x\right)=0\)
\(5x\left(x-1\right)+3\left(x-1\right)=0\)
\(\left(5x+3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+3=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{5}\\x=1\end{matrix}\right.\)
Vậy...
15 tháng 12 2017
\(5x\left(x-1\right)-3\left(1-x\right)=0\)
<=> \(5x\left(x-1\right)+3\left(x-1\right)=0\)
<=> \(\left(x-1\right)\left(5x+3\right)=0\)
<=> \(\left[{}\begin{matrix}x-1=0\\5x+3=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)
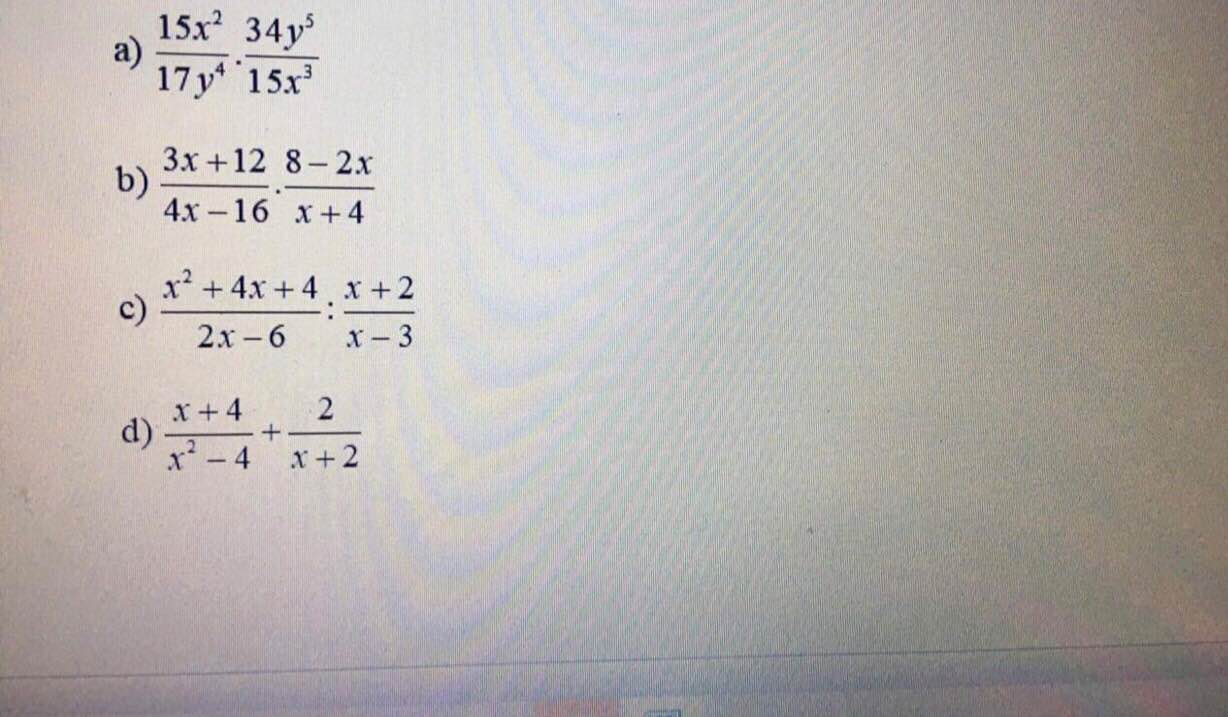
đề đâu