Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Ta có: \(A=\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\)
\(=\dfrac{4+6-3}{n-1}\)
\(=\dfrac{7}{n-1}\)
Để A là số tự nhiên thì \(7⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(7\right)\)
\(\Leftrightarrow n-1\in\left\{1;7\right\}\)
hay \(n\in\left\{2;8\right\}\)
Vậy: \(n\in\left\{2;8\right\}\)
ta có B=2n+9/n+2-3n+5n+1/n+2=4n+10/n+2 Để B là STN thì 4n+10⋮n+2 4n+8+2⋮n+2 4n+8⋮n+2 ⇒2⋮n+2 n+2∈Ư(2) Ư(2)={1;2} Vậy n=0

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

\(\dfrac{5}{3}\cdot\dfrac{7}{25}+\dfrac{5}{3}\cdot\dfrac{21}{25}-\dfrac{5}{3}\cdot\dfrac{7}{25}\)
\(=\dfrac{5}{3}\cdot\left(\dfrac{7.}{25}+\dfrac{21}{25}-\dfrac{7}{25}\right)\)
\(=\dfrac{5}{3}\cdot\dfrac{21}{25}=\dfrac{7}{5}\)
b) \(250\%+19\dfrac{3}{11}\cdot\dfrac{7}{26}-6\dfrac{3}{11}\cdot\dfrac{7}{26}\)
\(=\dfrac{5}{2}+\dfrac{212}{11}\cdot\dfrac{7}{26}-\dfrac{69}{11}\cdot\dfrac{7}{26}\)
\(=\dfrac{7}{26}\cdot\left(\dfrac{212}{11}-\dfrac{69}{11}\right)+\dfrac{5}{2}\)
\(=\dfrac{7}{26}\cdot13+\dfrac{5}{2}\)
\(=\dfrac{7}{2}+\dfrac{5}{2}\)
\(=\dfrac{12}{2}=6\)

(1) Để \(\dfrac{2n}{n-2}\) là số nguyên thì 2n⋮n-2
2n-4+4⋮n-2
2n-4⋮n-2⇒4⋮n-2
n-2∈Ư(4)⇒Ư(4)={1;-1;2;-2;4;-4}
n∈{3;1;4;0;6;-2}
(2) \(\dfrac{3}{10.12}+\dfrac{3}{12.14}+...+\dfrac{3}{48.50}\)
=\(\dfrac{3}{2}.\left(\dfrac{2}{10.12}+\dfrac{2}{12.14}+...+\dfrac{2}{48.50}\right)\)
=\(\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{14}+...+\dfrac{1}{48}-\dfrac{1}{50}\right)\)
=\(\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{50}\right)\)
=\(\dfrac{3}{2}.\dfrac{2}{25}\)
=\(\dfrac{3}{25}\)
Giải:
(1) Để \(\dfrac{2n}{n-2}\) là số nguyên thì \(2n⋮n-2\)
\(2n⋮n-2\)
\(\Rightarrow2n-4+4⋮n-2\)
\(\Rightarrow4⋮n-2\)
\(\Rightarrow n-2\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| n-2 | -4 | -2 | -1 | 1 | 2 | 4 |
| n | -2 | 0 | 1 | 3 | 4 | 6 |
| Kết luận | loại | t/m | t/m | t/m | t/m | t/m |
Vậy \(n\in\left\{0;1;3;4;6\right\}\)
(2) \(\dfrac{3}{10.12}+\dfrac{3}{12.14}+\dfrac{3}{14.16}+...+\dfrac{3}{48.50}\)
\(=\dfrac{3}{2}.\left(\dfrac{2}{10.12}+\dfrac{2}{12.14}+\dfrac{2}{14.16}+...+\dfrac{2}{48.50}\right)\)
\(=\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{16}+...+\dfrac{1}{48}-\dfrac{1}{50}\right)\)
\(=\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{50}\right)\)
\(=\dfrac{3}{2}.\dfrac{2}{25}\)
\(=\dfrac{3}{25}\)
Chúc bạn học tốt!

f: \(=\dfrac{7}{19}\left(\dfrac{8}{11}+\dfrac{3}{11}\right)-\dfrac{12}{19}=\dfrac{7}{19}-\dfrac{12}{19}=\dfrac{-5}{19}\)
i: \(=\left(\dfrac{9}{24}-\dfrac{18}{24}+\dfrac{14}{24}\right)\cdot\dfrac{6}{5}+\dfrac{1}{2}=\dfrac{5}{24}\cdot\dfrac{6}{5}+\dfrac{1}{2}\)
=1/4+1/2=3/4
` 7/19 . 8/11 + 3/11 . 7/19 + (-12)/19 `
`= 7/19 . ( 8/11 + 3/11 ) + (-12)/19 `
`= 7/19 . 11/11 + (-12)/19`
`= 7/19 . 1 + (-12)/19 `
`= 7/19 + (-12)/19 `
`= -5/19 `
`( 3/8 + (-3)/4 + 7/12 ) : 5/6 + 1/2`
`= 3/8 + (-3)4 + 7/12 . 6/5 + 1/2`
`= ( 9+(-18) + 14)/24 . 6/5 + 1/2`
`= 5/24 . 6/5 + 1/2`
`= 1/4 + 1/2 `
`= 3/4`



b: =>\(\dfrac{2}{2}+\dfrac{2}{6}+\dfrac{2}{12}+...+\dfrac{2}{n\left(n+1\right)}=\dfrac{200}{101}\)
=>\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{n\left(n+1\right)}=\dfrac{100}{101}\)
=>1-1/2+1/2-1/3+...+1/n-1/n+1=100/101
=>1-1/(n+1)=100/101
=>1/(n+1)=1/101
=>n+1=101
=>n=100
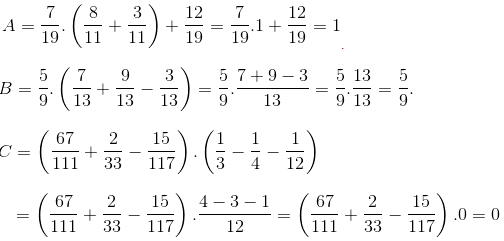
mk chỉ trả lời đk câu 1 thôi
\(\dfrac{3}{11}\). \(\dfrac{7}{19}\)
\(\dfrac{3}{11}\). \(\dfrac{7}{19}\)+ \(\dfrac{17}{11}\).\(\dfrac{3}{19}\)- \(\dfrac{3}{19}\). \(\dfrac{25}{11}\)
= \(\dfrac{3}{19}\). \(\dfrac{7}{11}\)+ \(\dfrac{17}{11}\).\(\dfrac{3}{19}\)- \(\dfrac{3}{19}\).\(\dfrac{25}{11}\)
= \(\dfrac{3}{19}\). ( \(\dfrac{7}{11}\)+ \(\dfrac{17}{11}\)- \(\dfrac{25}{11}\))
= \(\dfrac{3}{19}\). \(\dfrac{-1}{11}\)
= \(\dfrac{-3}{209}\)
mk chỉ lm đk bài này thôi, chúc bạn học tốt