Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=\dfrac{2}{10\cdot12}+\dfrac{2}{12\cdot14}+...+\dfrac{2}{98\cdot100}\)
\(S=\dfrac{2}{10}-\dfrac{2}{12}+\dfrac{2}{12}-\dfrac{2}{14}+...+\dfrac{2}{98}-\dfrac{2}{100}\)
\(S=\dfrac{2}{10}-\dfrac{2}{100}=\dfrac{9}{50}=0,18\)
Vậy \(S>\dfrac{1}{10}\)
\(S=\dfrac{2}{10\cdot12}+\dfrac{2}{12\cdot14}+\dfrac{2}{14\cdot16}+...+\dfrac{2}{98\cdot100}\)
\(S=\dfrac{2}{10}-\dfrac{2}{12}+\dfrac{2}{12}-\dfrac{2}{14}+...+\dfrac{2}{98}-\dfrac{2}{100}\)
\(S=\dfrac{2}{10}-\dfrac{2}{100}\)
\(S=\dfrac{20}{100}-\dfrac{2}{100}\)
\(S=\dfrac{18}{100}=\dfrac{9}{50}=0,18\)
\(\dfrac{1}{10}=0,1\), mà \(0,1< 0,18\)
\(\Rightarrow S>\dfrac{1}{10}\left(đpcm\right)\)

Bài 1:
a) \(\dfrac{2}{5}\cdot x-\dfrac{1}{4}=\dfrac{1}{10}\)
\(\dfrac{2}{5}\cdot x=\dfrac{1}{10}+\dfrac{1}{4}\)
\(\dfrac{2}{5}\cdot x=\dfrac{7}{20}\)
\(x=\dfrac{7}{20}:\dfrac{2}{5}\)
\(x=\dfrac{7}{8}\)
Vậy \(x=\dfrac{7}{8}\).
b) \(\dfrac{3}{5}=\dfrac{24}{x}\)
\(x=\dfrac{5\cdot24}{3}\)
\(x=40\)
Vậy \(x=40\).
c) \(\left(2x-3\right)^2=16\)
\(\left(2x-3\right)^2=4^2\)
\(\circledast\)TH1: \(2x-3=4\\ 2x=4+3\\ 2x=7\\ x=\dfrac{7}{2}\)
\(\circledast\)TH2: \(2x-3=-4\\ 2x=-4+3\\ 2x=-1\\ x=\dfrac{-1}{2}\)
Vậy \(x\in\left\{\dfrac{7}{2};\dfrac{-1}{2}\right\}\).
Bài 2:
a) \(25\%-4\dfrac{2}{5}+0.3:\dfrac{6}{5}\)
\(=\dfrac{1}{4}-\dfrac{22}{5}+\dfrac{3}{10}:\dfrac{6}{5}\)
\(=\dfrac{1}{4}-\dfrac{22}{5}+\dfrac{3}{10}\cdot\dfrac{5}{6}\)
\(=\dfrac{1}{4}-\dfrac{22}{5}+\dfrac{1}{4}\)
\(=\dfrac{5}{20}-\dfrac{88}{20}+\dfrac{5}{20}\)
\(=\dfrac{5-88+5}{20}\)
\(=\dfrac{78}{20}=\dfrac{39}{10}\)
b) \(\left(\dfrac{1}{6}-\dfrac{1}{5^2}\cdot5+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{1}{6}-\dfrac{1}{25}\cdot5+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{1}{6}-\dfrac{1}{5}+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{5}{30}-\dfrac{6}{30}+\dfrac{1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=\left(\dfrac{5-6+1}{30}\right)\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=0\cdot\left(\dfrac{2011}{2010}+\dfrac{2010}{1009}+\dfrac{2009}{2008}\right)\)
\(=0\)
Bài 3:
a) \(\dfrac{4}{19}\cdot\dfrac{-3}{7}+\dfrac{-3}{7}\cdot\dfrac{15}{19}\)
\(=\dfrac{-3}{7}\left(\dfrac{4}{19}+\dfrac{15}{19}\right)\)
\(=\dfrac{-3}{7}\cdot1\)
\(=\dfrac{-3}{7}\)
b) \(7\dfrac{5}{9}-\left(2\dfrac{3}{4}+3\dfrac{5}{9}\right)\)
\(=\dfrac{68}{9}-\dfrac{11}{4}-\dfrac{32}{9}\)
\(=\dfrac{68}{9}-\dfrac{32}{9}-\dfrac{11}{4}\)
\(=4-\dfrac{11}{4}\)
\(=\dfrac{16}{4}-\dfrac{11}{4}\)
\(\dfrac{5}{4}\)
Bài 4:
\(\dfrac{4}{12\cdot14}+\dfrac{4}{14\cdot16}+\dfrac{4}{16\cdot18}+...+\dfrac{4}{58\cdot60}\)
\(=2\left(\dfrac{1}{12\cdot14}+\dfrac{1}{14\cdot16}+\dfrac{1}{16\cdot18}+...+\dfrac{1}{58\cdot60}\right)\)
\(=2\left(\dfrac{1}{12}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{18}+...+\dfrac{1}{58}-\dfrac{1}{60}\right)\)
\(=2\left(\dfrac{1}{12}-\dfrac{1}{60}\right)\)
\(=2\left(\dfrac{5}{60}-\dfrac{1}{60}\right)\)
\(=2\cdot\dfrac{1}{15}\)
\(=\dfrac{2}{15}\)

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)
\(A=6-2\dfrac{4}{7}\)
\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)
\(A=3\dfrac{3}{7}\)
\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)
\(B=2+3\dfrac{7}{11}\)
\(B=5\dfrac{7}{11}\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{160}{11}\)
\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)
\(D=\dfrac{7}{28}=\dfrac{5}{2}\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)
\(\Rightarrow E=0\)

Bài 1:
a) \(\left(\dfrac{3}{8}+\dfrac{-3}{4}+\dfrac{7}{12}\right):\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\left(\dfrac{9}{24}+\dfrac{-18}{24}+\dfrac{14}{24}\right):\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\dfrac{5}{24}:\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\dfrac{5}{24}.\dfrac{6}{5}+\dfrac{1}{2}\)
\(=\dfrac{1}{4}+\dfrac{1}{2}\)
\(=\dfrac{1}{4}+\dfrac{2}{4}\)
\(=\dfrac{3}{4}\)
b) \(\dfrac{1}{2}+\dfrac{3}{4}-\left(\dfrac{3}{4}-\dfrac{4}{5}\right)\)
\(=\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{3}{4}+\dfrac{4}{5}\)
\(=\left(\dfrac{1}{2}+\dfrac{4}{5}\right)+\left(\dfrac{3}{4}-\dfrac{3}{4}\right)\)
\(=\dfrac{1}{2}+\dfrac{4}{5}\)
\(=\dfrac{5}{10}+\dfrac{8}{10}\)
\(=\dfrac{9}{5}\)
c) \(6\dfrac{5}{12}:2\dfrac{3}{4}+11\dfrac{1}{4}.\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}:\dfrac{11}{4}+\dfrac{42}{4}.\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}.\dfrac{4}{11}+\dfrac{42}{4}.\left(\dfrac{5}{15}+\dfrac{3}{15}\right)\)
\(=\dfrac{7}{3}+\dfrac{42}{4}.\dfrac{8}{15}\)
\(=\dfrac{7}{3}+\dfrac{14.2}{1.3}\)
\(=\dfrac{7}{3}+\dfrac{28}{3}\)
\(=\dfrac{35}{3}\)
d) \(\left(\dfrac{7}{8}-\dfrac{3}{4}\right).1\dfrac{1}{3}-\dfrac{2}{7}.\left(3,5\right)^2\)
\(=\left(\dfrac{7}{8}-\dfrac{6}{8}\right).\dfrac{4}{3}-\dfrac{2}{7}.12\dfrac{1}{4}\)
\(=\dfrac{1}{8}.\dfrac{4}{3}-\dfrac{2}{7}.\dfrac{49}{4}\)
\(=\dfrac{1}{6}-\dfrac{7}{2}\)
\(=\dfrac{1}{6}-\dfrac{21}{6}\)
\(=\dfrac{-10}{3}\)
e) \(\left(\dfrac{3}{5}+0,415-\dfrac{3}{200}\right).2\dfrac{2}{3}.0,25\)
\(=\left(\dfrac{3}{5}+\dfrac{83}{200}-\dfrac{3}{200}\right).\dfrac{8}{3}.\dfrac{1}{4}\)
\(=\left(\dfrac{120}{200}+\dfrac{83}{200}-\dfrac{3}{200}\right).\dfrac{8}{3}.\dfrac{1}{4}\)
\(=1.\dfrac{8}{3}.\dfrac{1}{4}\)
\(=\dfrac{2}{3}\)
f) \(\dfrac{5}{16}:0,125-\left(2\dfrac{1}{4}-0,6\right).\dfrac{10}{11}\)
\(=\dfrac{5}{16}:\dfrac{1}{8}-\left(\dfrac{9}{4}-\dfrac{3}{5}\right).\dfrac{10}{11}\)
\(=\dfrac{5}{16}.\dfrac{8}{1}-\left(\dfrac{45}{20}-\dfrac{12}{20}\right).\dfrac{10}{11}\)
\(=\dfrac{5}{2}-\dfrac{33}{20}.\dfrac{10}{11}\)
\(=\dfrac{5}{2}-\dfrac{3}{2}\)
\(=\dfrac{2}{2}=1\)
g) \(0,25:\left(10,3-9,8\right)-\dfrac{3}{4}\)
\(=\dfrac{1}{4}:\dfrac{1}{2}-\dfrac{3}{4}\)
\(=\dfrac{1}{4}.\dfrac{2}{1}-\dfrac{3}{4}\)
\(=\dfrac{1}{2}-\dfrac{3}{4}\)
\(=\dfrac{2}{4}-\dfrac{3}{4}\)
\(=\dfrac{-1}{4}\)
h) \(1\dfrac{13}{15}.0,75-\left(\dfrac{11}{20}+20\%\right):\dfrac{7}{3}\)
\(=\dfrac{28}{15}.\dfrac{3}{4}-\left(\dfrac{11}{20}+\dfrac{1}{5}\right):\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\left(\dfrac{11}{20}+\dfrac{4}{20}\right):\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\dfrac{3}{4}:\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\dfrac{9}{28}\)
\(=\dfrac{196}{140}-\dfrac{45}{140}\)
\(=\dfrac{151}{140}\)
i) \(\dfrac{\left(\dfrac{1}{2-0,75}\right).\left(0,2-\dfrac{2}{5}\right)}{\dfrac{5}{9}-1\dfrac{1}{12}}\)
\(=\dfrac{\left(\dfrac{1}{1,25}\right).\left(\dfrac{1}{5}-\dfrac{2}{5}\right)}{\dfrac{5}{9}-\dfrac{13}{12}}\)
\(=\dfrac{\dfrac{1}{1,25}.\dfrac{-1}{5}}{\dfrac{20}{36}-\dfrac{39}{36}}\)
\(=\dfrac{\dfrac{-1}{6,25}}{\dfrac{-19}{36}}\)
k) \(\dfrac{\dfrac{2}{3}+\dfrac{2}{7}-\dfrac{1}{14}}{-1-\dfrac{3}{7}+\dfrac{3}{28}}\)
\(=\dfrac{\dfrac{2}{3}+\dfrac{2}{7}-\dfrac{2}{28}}{-\dfrac{3}{3}-\dfrac{3}{7}+\dfrac{3}{28}}\)
\(=\dfrac{2\left(\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{28}\right)}{\left(-3\right)\left(\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{28}\right)}\)
\(=-\dfrac{2}{3}\)
\(A=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(A=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{3}{8}.\dfrac{5}{28}\)
\(A=\left(\dfrac{7}{10}.\dfrac{5}{28}\right).\left(\dfrac{8}{3}.\dfrac{3}{8}\right).20\)
\(A=\dfrac{1}{8}.1.20\)
\(A=\dfrac{20}{8}=\dfrac{5}{2}\)
\(B=\left(9\dfrac{30303}{80808}+7\dfrac{303030}{484848}\right)+4,03\)
\(B=\left(9\dfrac{3}{8}+7\dfrac{5}{8}\right)+4,03\)
\(B=\left[\left(9+7\right)+\left(\dfrac{3}{8}+\dfrac{5}{8}\right)\right]+4,03\)
\(B=\left(16+1\right)+4,03\)
\(B=17+4,03\)
\(B=21,03\)
\(C=\left(9,75.21\dfrac{3}{7}+\dfrac{39}{4}.18\dfrac{4}{7}\right).\dfrac{15}{78}\)
\(C=\left(\dfrac{39}{4}.\dfrac{150}{7}+\dfrac{39}{4}.\dfrac{130}{7}\right).\dfrac{15}{78}\)
\(C=\dfrac{39}{4}.\left(\dfrac{150}{7}+\dfrac{130}{7}\right).\dfrac{15}{78}\)
\(C=\dfrac{39}{4}.40.\dfrac{15}{78}\)
\(C=390.\dfrac{15}{78}\)
\(C=75\)

Đặt tổng trên là A ta có
\(2A=\frac{2}{10.12}+\frac{2}{12.14}+\frac{2}{14.16}+...+\frac{2}{48.52}\)
\(2A=\frac{12-10}{10.12}+\frac{14-12}{12.14}+\frac{16-14}{14.16}+...+\frac{50-48}{48.50}\)
\(2A=\frac{1}{10}-\frac{1}{12}+\frac{1}{12}-\frac{1}{14}+\frac{1}{14}-\frac{1}{16}+...+\frac{1}{48}-\frac{1}{50}=\frac{1}{10}-\frac{1}{50}=\frac{2}{25}\)
\(\Rightarrow A=\frac{2A}{2}=\frac{1}{25}\)

BÀi 1
Để A \(\in\) Z
=>\(\left(n+2\right)⋮\left(n-5\right)\)
=>\([\left(n-5\right)+7]⋮\left(n-5\right)\)
=>\(7⋮\left(n-5\right)\)
=>\(n-5\in\left\{1;7;-1;-7\right\}\)
=>\(n\in\left\{6;13;4;-2\right\}\)
Vậy \(n\in\left\{6;13;4;-2\right\}\)

A=\(\dfrac{3}{x-1}\)
Để \(\dfrac{3}{x-1}\) có giá trị nguyên thì
3\(⋮x-1\)
=> x-1\(\in\)Ư(3)=\(\left\{\pm3;\pm1\right\}\)
Ta có bảng sau:
| x-1 | 3 | -3 | 1 | -1 |
| x | 4 | -2 | 2 | 0 |
=> x\(\in\left\{4;\pm2;0\right\}\) (thỏa mãn x\(\in Z\))
Vậy để \(\dfrac{3}{x-1}\) có giá trị nguyên thì x\(\in\left\{4;\pm2;0\right\}\)
B=\(\dfrac{x-2}{x+3}\)
Để \(\dfrac{x-2}{x+3}\) có giá trị là số nguyên thì
\(x-2⋮x+3\)
<=> \(x+3-5⋮x+3\)
<=> -5\(⋮\)x+3
=> x+3\(\in\)Ư(-5)=\(\left\{\pm1;\pm5\right\}\)
Ta có bảng sau:
| x+3 | 1 | -1 | 5 | -5 |
| x | -2 | -4 | 2 | -8 |
=> x\(\in\left\{\pm2;-4;-8\right\}\) (thỏa mãn x\(\in Z\))
Vậy để\(\dfrac{x-2}{x+3}\) có giá trị nguyên thì x\(\in\left\{\pm2;-4;-8\right\}\)
C=\(\dfrac{2x+1}{x-3}\)
Để \(\dfrac{2x+1}{x-3}\) có giá trị là số nguyên thì
\(2x+1⋮x-3\)
<=> (x-3)+(x-3)+7\(⋮\)x-3
<=> 2(x-3)+7\(⋮\)x-3
<=> 7\(⋮x-3\)
=> x-3\(\inƯ_{\left(7\right)}=\left\{\pm1;\pm7\right\}\)
Ta có bảng sau:
| x-3 | 1 | -1 | 7 | -7 |
| x | 4 | 2 | 10 | -4 |
=> x\(\in\left\{\pm4;2;10\right\}\) (thỏa mãn x\(\in Z\))
Vậy để \(\dfrac{2x+1}{x-3}\) có giá trị là số nguyên thì x\(\in\left\{\pm4;2;10\right\}\)
D=\(\dfrac{x^2-1}{x+1}\)
Áp dụng hằng đẳng thức ta có:
\(\dfrac{x^2-1}{x+1}\) =\(\dfrac{\left(x-1\right)\left(x+1\right)}{x+1}\)= x-1
=> để x-1 có giá trị nguyên thì x\(\in Z\)
hay để \(\dfrac{x^2-1}{x+1}\) có giá trị nguyên thì x\(\in Z\)
Vậy để \(\dfrac{x^2-1}{x+1}\)có giá trị nguyên thì \(x\in Z\)

a) Gọi d là ƯCLN(n+1;2n+3)
=>n+1 chia hết cho d và 2n+3 chia hết cho d
=>2(n+1) chia hết cho d hay 2n+2 chia hết cho d
=>(2n+3)-(2n+2) chia hết cho d
hay 1 chia hết cho d
=>d=1
=> phân số \(\dfrac{n+1}{2n+3}\) tối giản với mọi số tự nhiên n
b) Gọi d là ƯCLN(4n+8;2n+3)
=>4n+8 chia hết cho d và 2n+3 chia hết cho d
=>2(n+3) chia hết cho d hay 4n+6 chia hết cho d
=>(4n+8)-(4n+6) chia hết cho d
hay 2 chia hết cho d
Do 2n+3=2(n+1)+1 không chia hết cho 2=>d phải là số lẻ và 2 chia hết cho d =>d=1
=> phân số \(\dfrac{2n+3}{4n+8}\) tối giản với mọi số tự nhiên n
Bạn vào đây nhé: Câu hỏi của Nguyễn Đinh Huyền Mai - Toán lớp 6 | Học trực tuyến
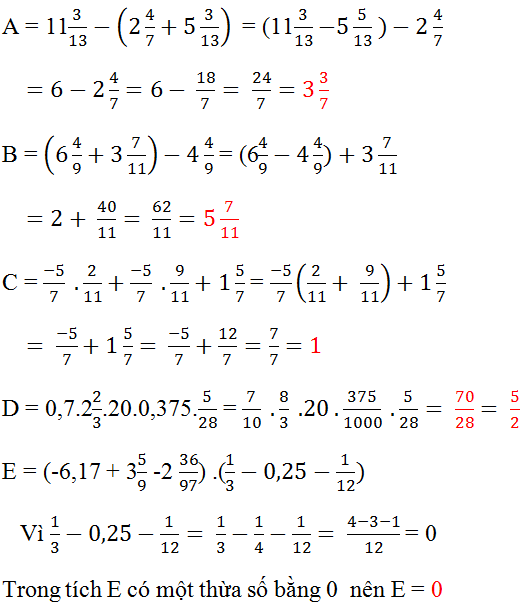
(1) Để \(\dfrac{2n}{n-2}\) là số nguyên thì 2n⋮n-2
2n-4+4⋮n-2
2n-4⋮n-2⇒4⋮n-2
n-2∈Ư(4)⇒Ư(4)={1;-1;2;-2;4;-4}
n∈{3;1;4;0;6;-2}
(2) \(\dfrac{3}{10.12}+\dfrac{3}{12.14}+...+\dfrac{3}{48.50}\)
=\(\dfrac{3}{2}.\left(\dfrac{2}{10.12}+\dfrac{2}{12.14}+...+\dfrac{2}{48.50}\right)\)
=\(\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{14}+...+\dfrac{1}{48}-\dfrac{1}{50}\right)\)
=\(\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{50}\right)\)
=\(\dfrac{3}{2}.\dfrac{2}{25}\)
=\(\dfrac{3}{25}\)
Giải:
(1) Để \(\dfrac{2n}{n-2}\) là số nguyên thì \(2n⋮n-2\)
\(2n⋮n-2\)
\(\Rightarrow2n-4+4⋮n-2\)
\(\Rightarrow4⋮n-2\)
\(\Rightarrow n-2\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Vậy \(n\in\left\{0;1;3;4;6\right\}\)
(2) \(\dfrac{3}{10.12}+\dfrac{3}{12.14}+\dfrac{3}{14.16}+...+\dfrac{3}{48.50}\)
\(=\dfrac{3}{2}.\left(\dfrac{2}{10.12}+\dfrac{2}{12.14}+\dfrac{2}{14.16}+...+\dfrac{2}{48.50}\right)\)
\(=\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{16}+...+\dfrac{1}{48}-\dfrac{1}{50}\right)\)
\(=\dfrac{3}{2}.\left(\dfrac{1}{10}-\dfrac{1}{50}\right)\)
\(=\dfrac{3}{2}.\dfrac{2}{25}\)
\(=\dfrac{3}{25}\)
Chúc bạn học tốt!