K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 11 2016
\(A=2^{2014}-2^{2013}-2^{2012}-......-2^2-2-1\)
\(\Rightarrow\left(-2\right)\times A=-2^{2015}+2^{2014}+2^{2013}+.....+2^3+2^2+2\)
\(\Rightarrow-2A+A=-A=-2^{2015}-1=-\left(2^{2015}+1\right)\)
\(\Rightarrow A=2^{2015}+1\)
12 tháng 3 2019
\(\frac{\frac{1}{2012}+\frac{1}{2013}-\frac{1}{2014}}{\frac{5}{2012}+\frac{5}{2013}-\frac{5}{2014}}-\frac{\frac{2}{2013}+\frac{2}{2014}-\frac{2}{2015}}{\frac{3}{2013}+\frac{3}{2014}-\frac{3}{2015}}\)
=\(\frac{\frac{1}{2012}+\frac{1}{2013}-\frac{1}{2014}}{5\left(\frac{1}{2012}+\frac{1}{2013}-\frac{1}{2014}\right)}-\frac{2\left(\frac{1}{2013}+\frac{1}{2014}-\frac{1}{2015}\right)}{3\left(\frac{1}{2013}+\frac{1}{2014}-\frac{1}{2015}\right)}=\frac{1}{5}-\frac{2}{3}=\frac{3}{15}-\frac{10}{15}=-\frac{7}{15}\)
BP
30 tháng 8 2023
A= 1+(\(\dfrac{1}{2014}\)+1)+(\(\dfrac{2}{2013}\)+1)+...+(\(\dfrac{2013}{2}\)+1)
= \(\dfrac{2015}{2015}\)+(\(\dfrac{1}{2014}\)+1)+(\(\dfrac{2}{2013}\)+1)+...+(\(\dfrac{2013}{2}\)+1)
= 2015.(\(\dfrac{1}{2015}\)+\(\dfrac{1}{2014}\)+\(\dfrac{1}{2013}\)+...+\(\dfrac{1}{2}\))=2015.B
\(\Rightarrow\) \(\dfrac{A}{B}\)=2015
CT
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 4 2023
S = 1 - 2 + 22 - 23+.....+ 22012 - 22013
2\(\times\)S = 2 - 22 + 23-.......- 22012 + 22013 - 22014
2 \(\times\) S + S = 1 - 22014
3S = 1 - 22014
3S - 22014 = 1 - 22014 - 22014 = 1 - 2.22014 = 1- 22015
PT
1
PT
1
HL
26 tháng 3 2017
\(TA-CO':\)
\(A=\frac{4+\frac{7}{2014}-\frac{7}{2015}+\frac{7}{2012}-\frac{7}{2013}}{7+\frac{7}{2014}-\frac{7}{2015}+\frac{7}{2012}-\frac{7}{2013}}\)
\(A=\frac{4\left(\frac{1}{2014}-\frac{1}{2015}+\frac{1}{2012}-\frac{1}{2013}\right)}{7\left(\frac{1}{2014}-\frac{1}{2015}+\frac{1}{2012}-\frac{1}{2013}\right)}\)
\(A=\frac{4}{7}\)
\(B=\frac{1+2+...+2^{2013}}{2^{2015}-2}\)
ĐẶT \(C=1+2+...+2^{2013}\)
\(\Rightarrow2C=2+2^2+...+2^{2014}\)
\(\Rightarrow2C-C=\left(2+2^2+...+2^{2014}\right)-\left(1+2+...+2^{2013}\right)\)
\(\Rightarrow C=2^{2014}-2\)
\(\Rightarrow B=\frac{2^{2014}-1}{2^{2015}-2}\)
\(B=\frac{2^{2014}-1}{2\left(2^{2014}-1\right)}\)
\(B=\frac{1}{2}\)
\(\Rightarrow A-B=\frac{3}{7}-\frac{1}{2}=\frac{6}{14}-\frac{7}{14}\)
\(A-B=\frac{6-7}{14}=\frac{-1}{14}\)
VẬY, \(A-B=\frac{-1}{14}\)
28 tháng 2 2022
Đặt \(B=2^{2013}+2^{2012}+...+2^2+2+1\)
\(\Leftrightarrow A=2^{2014}-B\)
Ta có: \(B=2^{2013}+2^{2012}+...+2^2+2+1\)
\(\Leftrightarrow2B=2^{2014}+2^{2013}+...+2^3+2^2+2\)
\(\Leftrightarrow B=2^{2014}-1\)
\(\Leftrightarrow A=2^{2014}-B=2^{2014}-2^{2014}+1=1\)
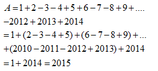
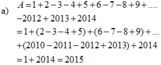
A=22014-22013-22012-...-22-2-1
2A=22015-22014-22012-...-23-22-2
2A-A=(22015-22014-22013-...-23-22-2)-(22014-22013-22012-...-22-2-1)
A=22015-1
Mình không biết