K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 7 2021
\(101^2=\left(100+1\right)^2=10000+200+1=10201\)
\(1001^2=\left(1000+1\right)^2=1000000+2000+1=1002001\)
\(102^2=\left(100+2\right)^2=10000+400+4=10404\)
\(99^2=\left(100-1\right)^2=10000-200+1=9801\)
\(19^2=\left(10+9\right)^2=100+180+81=361\)
\(999^2=\left(1000-1\right)^2=1000000-2000+1=998001\)
23 tháng 1 2021
2) Ta có: \(\dfrac{59-x}{19}+\dfrac{58-x}{18}=\dfrac{57-x}{17}+\dfrac{56-x}{16}\)
\(\Leftrightarrow\dfrac{59-x}{19}-1+\dfrac{58-x}{18}-1=\dfrac{57-x}{17}-1=\dfrac{56-x}{16}-1\)
\(\Leftrightarrow\dfrac{40-x}{19}+\dfrac{40-x}{18}-\dfrac{40-x}{17}-\dfrac{40-x}{16}=0\)
\(\Leftrightarrow\left(40-x\right)\left(\dfrac{1}{19}+\dfrac{1}{18}-\dfrac{1}{17}-\dfrac{1}{16}\right)=0\)
mà \(\dfrac{1}{19}+\dfrac{1}{18}-\dfrac{1}{17}-\dfrac{1}{16}\ne0\)
nên 40-x=0
hay x=40
Vậy: x=40
20 tháng 2 2021
Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(\Leftrightarrow AC=\sqrt{192}\cdot\cot60^0=8\left(cm\right)\)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\sqrt{3}\cdot8}{2}=32\sqrt{3}\left(cm^2\right)\)
O
1
20 tháng 7 2023
`a, 126^2 - 152 . 126 + 5776.`
`= 126^2 - 2 . 76 . 126 + 76^2`
`= (126+76)^2 = 202^2 = 40804`
`b, 3^8 . 5^8 - (15^4-1)(15^4+1)`
`= 15^8 - 15^8 + 1`
`= 1`
1 tháng 7 2021
Chắc là \(+28^2\)
Ta có : \(A=\left(30-29\right)\left(30+29\right)+.....+\left(2-1\right)\left(2+1\right)\)
\(=30+29+28+...+2+1\)
\(=465< 600\)
Vậy ....
1 tháng 7 2021
Sửa đề: \(A=30^2-29^2+28^2-27^2+...+2^2-1^2\)
\(=30+29+28+27+...+2+1\)
\(=465< 600\)
Vậy: A<600
NH
1
VQ
26 tháng 1 2016
AB^2+AC^2=BC^2
AC^2+ CĂN 192=4AC^2 (VÌ AC =1/2 BC)
SUY RA 3AC^2=CĂN 192
SUY RA AC^2=\(\frac{\sqrt{192}}{3}\)
SUY RA AC=
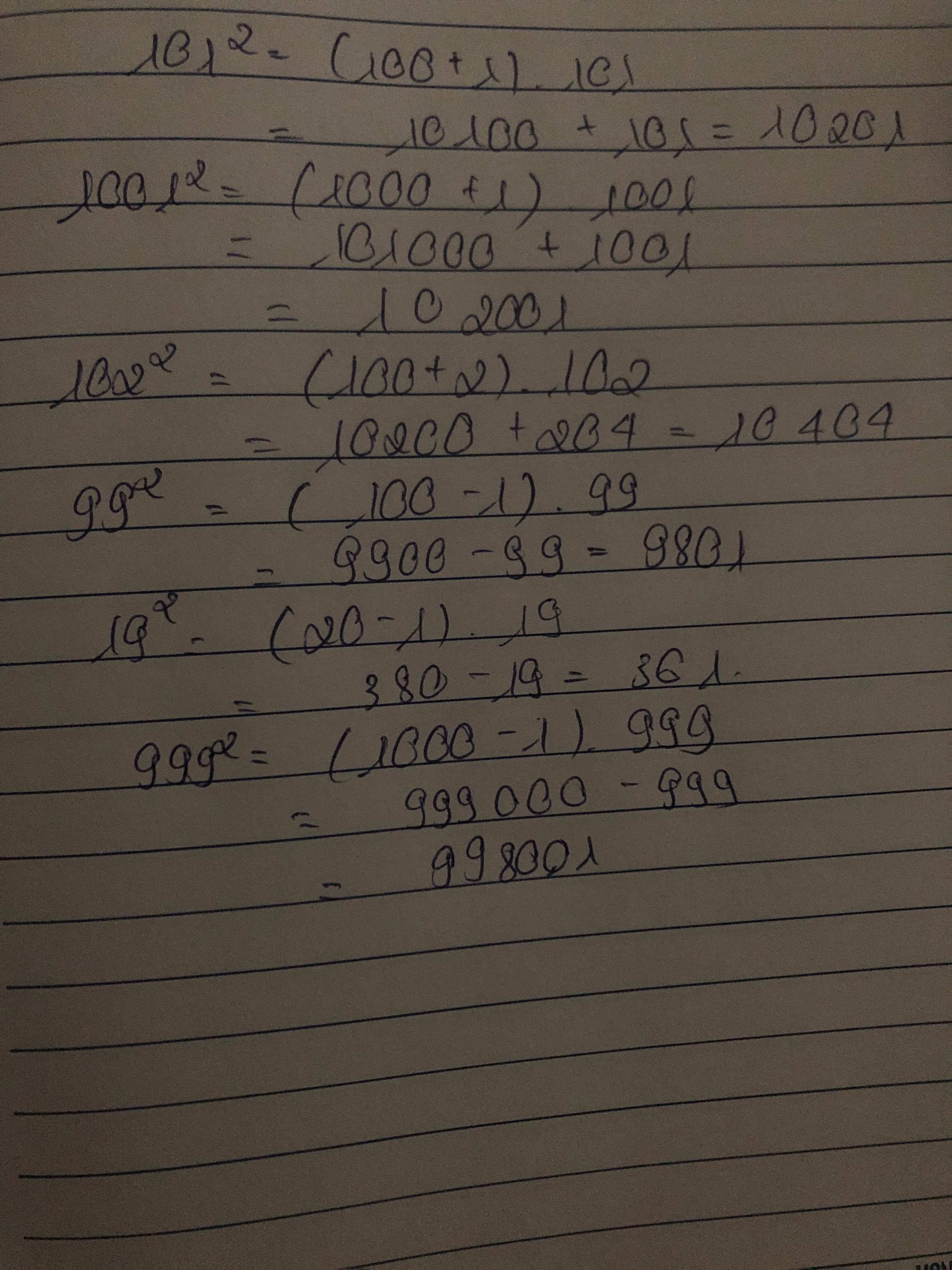
29^2 - 58 . 19 + 19^2
= 841 - 1102 + 361
= 100
\(29^2-58.19+19^2\)
\(=841-1102+361\)
\(=-261+361\)
\(=100\)