K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 8 2023
1: \(\Leftrightarrow\left(x-1\right)^x\cdot\left(x-1\right)^2-\left(x-1\right)^x=0\)
=>\(\left(x-1\right)^x\cdot\left[\left(x-1\right)^2-1\right]=0\)
=>\(x\left(x-1-1\right)\cdot\left(x-1\right)^x=0\)
=>x(x-2)(x-1)^x=0
=>x=0;x=2;x=1
2: \(\Leftrightarrow\left(6-x\right)^{2003}\left(x-1\right)=0\)
=>6-x=0 hoặc x-1=0
=>x=6;x=1
3: =>(7x-11)^3=32*25+200=1000
=>7x-11=10
=>7x=21
=>x=3
4: =>x^2-1=-3 hoặc x^2-1=3
=>x^2=-2(loại) hoặc x^2=4
=>x=2 hoặc x=-2
10 tháng 8 2021
\(x^2-4⋮x-1\)
Ta có : \(x^2-4=\left(x^2-1\right)-3\)
Vì \(x^2-1⋮x-1\) nên \(4⋮x-1\\ \Rightarrow x-1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\Rightarrow x-1\in\left\{2;0;3;-1;5;-3\right\}\)
bạn tick cho mình với
17 tháng 10 2021
\(\left(3-x\right)\left(x^2+1\right)=0\)
\(\Rightarrow x=3\)(do \(x^2+1\ge1>0\forall x\))
KH
1
13 tháng 12 2022
\(\Leftrightarrow4⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2;4;-4\right\}\)
mà x là số tự nhiên
nên \(x\in\left\{2;0;3;5\right\}\)
TG
1
14 tháng 10 2021
a) \(\Rightarrow x^2=16\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
b) \(\Rightarrow\left(x-1\right)^3=27\Rightarrow x-1=3\Rightarrow x=4\)
c) \(\Rightarrow3^x.3^3=3^{12}\)
\(\Rightarrow3^x=3^9\Rightarrow x=9\)
CM
8 tháng 9 2018
a) Ta có: x 2 = 2 2 nên x = 2.
b) Ta có: x 2 = 5 2 nên x = 5.
c) Ta có: 3 x 5 = 3 nên x 5 = 1 . Do đó x = 1.
d) Ta có: 6 x 3 = 48 nên x 3 = 8 . Do đó x = 2.
e) Ta có: x - 1 2 = 2 2 nên x - 1 = 2 . Do đó x = 3.
f) Ta có: x + 1 2 = 5 2 nên x +1 = 5. Do đó x = 4.
g) Ta có: x - 1 3 = 3 3 nên x - 1 = 3 . Do đó x = 4.
h) Ta có: x + 1 3 = 4 3 nên x +1 = 4. Do đó x = 3
VH
1
20 tháng 3 2020
a) (x2-1)(x2-4)<0
=> x2-1 và x2-4 trái dấu nhau
Ta thấy: x2 >=0 với mọi x => x2-1 > x2-4
=> \(\hept{\begin{cases}x^2-1>0\\x^2-4< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2>1\\x^2< 4\end{cases}\Leftrightarrow}\hept{\begin{cases}x>\pm1\\x< \pm2\end{cases}}}\)
=> Không có giá trị củ x thỏa mãn đề bài
NH
0
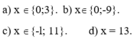
Ta có : (x2 - x - 1) chia hết cho (x - 1)
=> x(x - 1) - 1 chia hết cho x - 1
=> 1 chia hết cho x - 1
=> x - 1 thuộc Ư(1) {-1;1}
Ta có bảng :
Aikatsu Stars
Ta có : ﴾x 2 ‐ x ‐ 1﴿ chia hết cho ﴾x ‐ 1﴿
=> x﴾x ‐ 1﴿ ‐ 1 chia hết cho x ‐ 1
=> 1 chia hết cho x ‐ 1
=> x ‐ 1 thuộc Ư﴾1﴿ {‐1;1}
Ta có bảng :