
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

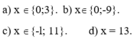

a) \(\left(x^2-5\right)\left(x^2-25\right)< 0\)
Vì \(x^2-5>x^2-25\) nên \(\left\{{}\begin{matrix}x^2-5>0\\x^2-25< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2>5\\x^2< 25\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{5}< x< -\sqrt{5}\left(vl\right)\\-5< x< 5\end{matrix}\right.\)
b) \(\left(x+5\right)\left(9+x^2\right)< 0\)
Vì \(9+x^2>0\) nên \(x+5< 0\Leftrightarrow x< -5\)
c) \(\left(x+3\right)\left(x^2+1\right)=0\)
Vì \(x^2+1>0\) nên \(x+3=0\Leftrightarrow x=-3\)
d) \(\left(x+5\right)\left(x^2-4\right)=0\)
\(\Rightarrow\left(x+5\right)\left(x+2\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=-2\\x=2\end{matrix}\right.\)

a)
\(\left|x\right|-2\left|x\right|+3\left|x\right|=16+6\left|x\right|-19\)
\(\left|x\right|-2\left|x\right|+3\left|x\right|-6\left|x\right|=16-19\)
\(\left|x\right|.\left(1-2+3-6\right)=-3\)
\(\left|x\right|.\left(-4\right)=-3\)
\(\left|x\right|=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=\dfrac{3}{4}\end{matrix}\right.\)
b,
2.(|x| - 5) - 15 = 9
\(2.\left(\left|x\right|-5\right)=9+15\)
\(2.\left(\left|x\right|-5\right)=24\)
\(\left|x\right|-5=24:2\)
\(\left|x\right|-5=12\)
\(\left|x\right|=12+5\)
\(\left|x\right|=17\)
\(\Rightarrow\left[{}\begin{matrix}x=-17\\x=17\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=-17\\x=17\end{matrix}\right.\)
c,
|8 - 2x| + |4y - 16| = 0
\(\Rightarrow\left\{{}\begin{matrix}\left|8-2x\right|=0\\\left|4y-16\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}8-2x=0\\4y-16=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=8\\4y=16\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=4\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=4\\y=4\end{matrix}\right.\)
d,
|x - 14| + |2y - x| = 0
\(\Rightarrow\left\{{}\begin{matrix}\left|x-14\right|=0\\\left|2y-x\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-14=0\\2y-x=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=14\\2y=x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=14\\2y=14\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=14\\y=7\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=14\\y=7\end{matrix}\right.\)
2.Tìm x, y, z biết
a,
2.|3x| + |y + 3| + |z - y| = 0
\(\Rightarrow\left\{{}\begin{matrix}2.\left|3x\right|=0\\\left|y+3\right|=0\\\left|z-y\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|3x\right|=0\\y+3=0\\z-y=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x=0\\y=-3\\z=y\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-3\\z=-3\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=0\\y=-3\\z=-3\end{matrix}\right.\)
b, (x - 3y)2 + | y + 4|= 0
\(\Rightarrow\left\{{}\begin{matrix}\left(x-3y\right)2=0\\\left|y+4\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-3y=0\\y+4=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=3y\\y=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.\left(-4\right)\\y=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-12\\y=-4\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=-12\\y=-4\end{matrix}\right.\)

\(a.\left(x-4\right)\left(x+7\right)=0\)
\(\Rightarrow\hept{\begin{cases}x-4=0\\x+7=0\end{cases}\Rightarrow\hept{\begin{cases}x=4\\x=-7\end{cases}}}\)
\(b.x\left(x+3\right)=0\)
\(\Rightarrow\hept{\begin{cases}x=0\\x+3=0\end{cases}\Rightarrow\hept{\begin{cases}x=0\\x=-3\end{cases}}}\)
\(c.\left(x-2\right)\left(5-x\right)=0\)
\(\Rightarrow\hept{\begin{cases}x-2=0\\5-x=0\end{cases}\Rightarrow\hept{\begin{cases}x=2\\x=5\end{cases}}}\)
\(d.\left(x-1\right)\left(x^2+1\right)=0\)
\(\Rightarrow\hept{\begin{cases}x-1=0\\x^2+1=0\end{cases}\Rightarrow\hept{\begin{cases}x=1\\x^2=-1\end{cases}\Rightarrow}\hept{\begin{cases}x=1\\x=-\left(-1\right)or\left(-1\right)\end{cases}}}\)
a) ( x - 4 ) . ( x + 7 ) = 0
một phép nhân có tích bằng 0
=> một trong hai thừa số này bằng 0
+) nếu x - 4 = 0 => x = 0 + 4 = 4
+) nếu x + 7 = 0 => x = 0 - 7 = -7
vậy x = { 4 ; -7 }
b) x . ( x + 3 ) = 0
x + 3 = 0 : x
x + 3 = 0
x = 0 - 3
x = -3
vậy x = -3
c) ( x - 2 ) . ( 5 - x ) = 0
một phép nhân có tích bằng 0
=> một trong hai thừa số này bằng 0
+) nếu x - 2 = 0 => x = 0 + 2 = 2
+) nếu 5 - x = 0 => x = 5 - 0 = 5
vậy x = { 2 ; 5 }
d) ( x - 1 ) . ( x2 + 1 ) = 0
=> x - 1 = 0 hoặc x2 + 1 = 0
+) x - 1 = 0 => x = 0 + 1 = 1
+) x2 + 1 = 0 => x2 = 0 - 1 = -1 => x = -1
vậy x = { 1 ; -1 }

bài 2) a) \(2\left(x+1\right)=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\) vậy \(x=-1\)
b) \(x\left(x-2\right)=0\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\end{matrix}\right.\) vậy \(x=0;x=2\)
c) \(\left(x-1\right)\left(x+7\right)=0\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\x+7=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\) vậy \(x=1;x=-7\)
d) \(\left(x+2\right)\left(x^2-9\right)=0\Leftrightarrow\left\{{}\begin{matrix}x+2=0\\x^2-9=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\x^2=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\\left\{{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\end{matrix}\right.\) vậy \(x=-2;x=3;x=-3\)
e) \(x^2\left(x-5\right)+2\left(x-5\right)=0\Leftrightarrow\left(x^2+2\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2=0\\x-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\in\varnothing\\x=5\end{matrix}\right.\) vậy \(x=5\)
bài 1) \(A=48+\left(-48-174\right)+\left|-74\right|=48-48-174+74=-100\)
\(B=\left(-123\right)+77+\left(-257\right)-23-43=-123+77-257-23-43=-369\)
\(C=\left(-57\right)+\left(-159\right)+47+169=-57-159+47+169=0\)
quá hợp lí ![]()

a) \(\left(x-4\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x-4=0\\x-7=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=4\\x=7\end{array}\right.\)
b) \(x\left(x+3\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\x+3=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\x=-3\end{array}\right.\)
c) \(\left(x-2\right)\left(5-x\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x-2=0\\5-x=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=2\\x=5\end{array}\right.\)
d) \(\left(x-1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x-1=0\) ( Vì \(x^2+1>0\) )
\(\Leftrightarrow x=1\)
a)
\(\left(x-4\right)\left(x-7\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=4\\x=7\end{array}\right.\)
Vậy x = 4 ; x = 7
b)
\(x\left(x+3\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=0\\x=-3\end{array}\right.\)
Vậy x = 0 ; x = - 3
c)
\(\left(x-2\right)\left(5-x\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=2\\x=5\end{array}\right.\)
Vậy x = 2 ; x = 5
d)
\(\left(x-1\right)\left(x^2+1\right)=0\)
Mà \(x^2+1\ge1\)
=> x = - 1
Vậy x = - 1

a/ => (x2 - 5)(x + 5)(x - 5) = 0
=> x2 - 5 = 0 => x2 = 5 => x = \(+-\sqrt{5}\) (loại)
hoặc x + 5 = 0 => x = -5
hoặc x - 5 = 0 => x = 5
Vậy x = 5 ; x = -5
b/ => x + 5 = 0 => x = -5
hoặc 9 + x2 = 0 => x2 = -9 (vô nghiệm)
Vậy x = -5
c/ => x + 3 = 0 => x = -3
hoặc x2 + 1 = 0 => x2 = -1 (vô nghiệm)
Vậy x = -3
d/ => (x + 5)(x + 2)(x - 2) = 0
=> x + 5 = 0 => x = -5
hoặc x + 2 = 0 => x = -2
hoặc x - 2 = 0 => x = 2
Vậy x = -5 ; x = -2; x = 2

B1: a, |2 - x| + 2 = x
=> |2 - x| = x - 2
Dễ thấy (2 - x) và số đối của (x - 2)
=> |2 - x| = x - 2
=> 2 - x ≤ 0
=> x ≥ 2
b, Điều kiện: x + 7 ≥ 0 => x ≥ -7
Ta có: |x - 9| = x + 7
\(\Rightarrow\orbr{\begin{cases}x-9=x+7\\x-9=-x-7\end{cases}\Rightarrow}\orbr{\begin{cases}0x=16\left(loai\right)\\2x=2\end{cases}\Rightarrow x=1}\left(t/m\right)\)