

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



6.
\(cos\sqrt{x+\dfrac{\pi}{4}}\in\left[-1;1\right]\)
\(\Rightarrow-5\le5cos\sqrt{x+\dfrac{\pi}{4}}\le5\)
\(\Leftrightarrow-5\le y\le5\)
\(\Rightarrow miny=-5\Leftrightarrow cos\sqrt{x+\dfrac{\pi}{4}}=-1\Leftrightarrow\sqrt{x+\dfrac{\pi}{4}}=\pi+k2\pi\Leftrightarrow...\)
\(maxy=5\Leftrightarrow cos\sqrt{x+\dfrac{\pi}{4}}=1\Leftrightarrow\sqrt{x+\dfrac{\pi}{4}}=k2\pi\Leftrightarrow...\)

\(y=-1-cos^2\left(2x+\dfrac{\pi}{3}\right)\)
\(=-\dfrac{3}{2}+\dfrac{1}{2}-cos^2\left(2x+\dfrac{\pi}{3}\right)\)
\(=-\dfrac{3}{2}-\dfrac{1}{2}\left[2cos^2\left(2x+\dfrac{\pi}{3}\right)-1\right]\)
\(=-\dfrac{3}{2}-\dfrac{1}{2}cos\left(4x+\dfrac{2\pi}{3}\right)\)
Vì \(cos\left(4x+\dfrac{2\pi}{3}\right)\in\left[-1;1\right]\)
\(\Rightarrow min=-\dfrac{3}{2}-\dfrac{1}{2}=-2\Leftrightarrow cos\left(4x+\dfrac{2\pi}{3}\right)=1\)
\(\Rightarrow max=-\dfrac{3}{2}+\dfrac{1}{2}=-1\Leftrightarrow cos\left(4x+\dfrac{2\pi}{3}\right)=-1\)

a, Do \(-1\le sin\alpha\le1\Rightarrow-0,3\le v_x=0,3sin\alpha\le0,3\)
Vậy giá trị lớn nhất của \(v_x\) là 0,3m/s và giá trị nhỏ nhất là -0,3m/s
b, Ta có đồ thị hàm số:
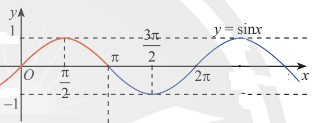
Với góc \(\alpha\in\left(0;\dfrac{\pi}{2}\right)\) hoặc \(\alpha\in\left(\dfrac{3\pi}{2};2\pi\right)\) thì \(v_x\) tăng.

Tham khảo
y = 4sin √ x ( đk x ≥ 0 )
ta thấy: -1 ≤ sin √ x ≤ 1
<=> -4 ≤ 4sin √ x ≤ 4
<=> -4 ≤ y ≤ 4
max y = 4
dấu "=" xảy ra <=> sin √ x = 1
<=> √ x = pi/2 +2kpi
<=> x = (pi/2 +2kpi )^2
min y = -4
dấu "=" xảy ra <=> sin √ x = -1
<=> √ x = -pi/2 +2kpi
<=> x = (-pi/2 +2kpi)^2
a. \(y=2cos\left(x+\dfrac{\pi}{3}\right)+3\)
Ta có: \(-1\le cos\alpha\le1\)
\(\Leftrightarrow-2\le2cos\alpha\le2\)
\(\Leftrightarrow-2+3\le2cos\alpha+3\le2+3\)
\(\Leftrightarrow1\le2cos\alpha+3\le5\)
Vậy y đạt GTNN ymin=1 khi \(\left[{}\begin{matrix}x=\dfrac{2}{3}\pi+k2\pi\\x=\dfrac{-4}{3}\pi+k2\pi\end{matrix}\right.\) và y đạt GTLN khi ymax=5 khi \(x=-\dfrac{\pi}{3}+k2\pi\)

\(y=\sqrt{3}sin2x-cos2x=2\left(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x\right)=2sin\left(2x-\dfrac{\pi}{6}\right)\)
Do \(-1\le sin\left(2x-\dfrac{\pi}{6}\right)\le1\Rightarrow-2\le y\le2\)
\(y_{max}=2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(y_{min}=-2\) khi \(sin\left(2x-\dfrac{\pi}{6}\right)=-1\)