Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔHIK có IN là phân giác
nên HN/NK=HI/IK=HK/IK(1)
Xét ΔHIK có KM là phân giác
nên HM/MI=HK/KI(2)
Từ (1) và (2) suy ra HN/NK=HM/MI
=>MN//IK
=>ΔHMN\(\sim\)ΔHIK
b: Ta có: HN/HI=NK/IK
=>HN/10=NK/8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{HN}{5}=\dfrac{NK}{4}=\dfrac{HN+NK}{5+4}=\dfrac{10}{9}\)
Do đó: HN=50/9(cm)
Xét ΔHIK có MN//IK
nên MN/IK=HN/HK
\(\Leftrightarrow MN=\dfrac{50}{9}:10\cdot8=\dfrac{40}{9}\left(cm\right)\)

a: Xét tứ giác HGEN có
HG//EN
HN//GE
Do đó: HGEN là hình bình hành
mà HE là tia phân giác
nên HGEN là hình thoi

a: Xét ΔHKI có
M là trung điểm của HI
MF//IK
Do đó: F là trung điểm của HK
Xét ΔHKI có
M là trung điểm của HI
F là trung điểm của HK
Do đó: MF là đường trung bình của ΔHKI
Suy ra: \(MF=\dfrac{IK}{2}=\dfrac{18}{2}=9\left(cm\right)\)
b: Xét tứ giác MFKI có MF//IK
nên MFKI là hình thang

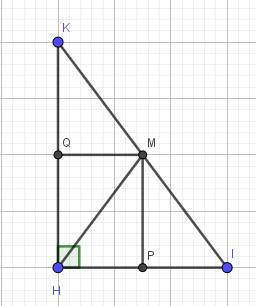
a) Do MP // HK (gt)
\(HK\perp HI\) (\(\Delta HIK\) vuông tại H)
\(\Rightarrow MP\perp HI\)
\(\Rightarrow\widehat{MPH}=90^0\)
Do MQ // HI (gt)
\(HI\perp HK\left(cmt\right)\)
\(\Rightarrow MQ\perp HK\)
\(\Rightarrow\widehat{MQH}=90^0\)
Tứ giác HQMP có:
\(\widehat{MQH}=\widehat{MPH}=\widehat{PAQ}=90^0\)
\(\Rightarrow HQMP\) là hình chữ nhật
b) \(\Delta MPH\) vuông tại P
\(\Rightarrow HM^2=PM^2+PH^2\left(Pytago\right)\)
\(\Rightarrow PM^2=HM^2-PH^2=10^2-6^2=64\)
\(\Rightarrow PM=8\left(cm\right)\)
Diện tích HQMP:
\(S_{HQMP}=PM.PH=8.6=48\left(cm^2\right)\)

Do \(\Delta ABC\) đồng dạng với \(\Delta HIK\)
\(\Rightarrow\frac{AB}{IH}=\frac{BC}{IK}=\frac{AC}{HK}\)
\(\Leftrightarrow\frac{7}{14}=\frac{9}{IK}=\frac{AC}{16}\)
\(\Leftrightarrow\hept{\begin{cases}IK=18\\AC=8\end{cases}}\)
Khi đó :
+) Chu vi \(\Delta ABC\) là : \(AB+BC+CA=7+9+8=24\left(cm\right)\)
+) Chu vi \(\Delta HIK\) là : \(HI+IK+KH=14+18+16=48\left(cm\right)\)
a: Xét ΔHIK và ΔHNM có
HI/HN=HK/HM=5/2
góc H chung
=>ΔHIK đồng dạng với ΔHNM
b:
ΔHIK đồng dạng với ΔHNM
=>IK/NM=5/2
=>10/NM=5/2
=>NM=4cm
c: Xét ΔHIK và ΔHAI có
góc HIK=góc HAI(=góc HNM)
góc Hchung
=>ΔHIK đồng dạng với ΔHAI