Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
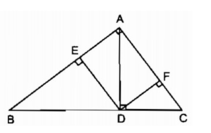
DE và CA cùng vuông góc với AB, do đó
DE // AC.
Theo định lí Ta-lét, ta có:
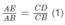
Tương tự, ta có: DF // AB, do đó:
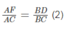
Cộng các vế tương ứng của (1) và (2), ta có:
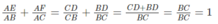
Tổng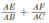 
không thay đổi vì luôn có giá trị bằng 1.
Vậy : Khi độ dài cạnh góc vuông AB, AC của tam giác vuông ABC thay đổi thì tổng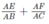 
luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.
a: Xet ΔABC vuông tại A và ΔHBA vuông tại H co
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
Hình tự vẽ dc ko ạ =(((( mik vẽ r nhưng lại bị out ra =.= lười lắm ạ
A/ xét tg AEHF ta có : HE vuông góc AB, FA vuông góc AB, HE//AC (gt)
=> góc AEH = góc EAF = góc AFH = 90 độ
=> Tứ giác AEHF là HCN
=>AH=EF
B/ Ta có H đối xứng M qua E => ME=EH
mak EH= AF (hcn) => ME=À
Ta có H đối xứng vs N qua F => FH=FN
mak FH =EA (hcn) => FN=EA
Xét tứ giác MEFA có :
+ ME=AF
+ ME//AF( slt)
=>Tứ giác MEFA là hình bình hành
=>EF=MA,EF//MA (1)
Xét tứ giác EFAN có :
+ FN = EA
+ AE//FN (slt)
=>Tứ giác EFAN là hình bình hành
=>EF=AN.EF//AN(2)
Từ (1) và (2) => MA=AN ; A,M,N thẳng hàng
=> M đối xứng N qua A
Ak quên câu C =.= ko thấy .V
C/Ta có M đối xứng H qua AB
=> AB là đg trung trực
=>MB=HB;MA=HA
Xét tam giác ABM và tam giác HAB có
BM=BH
MA=MH
AB chung
=>tam giác ABM = tam giác HAB (c-c-c)
=) góc M = góc H =90độ
Ta có H đối xứng N qua AC
=> AC là đg trung trực
=>HC=CN;HA=AN
Xét tam giác HCA và Tam giác ACN
HC=CN
HA=AN
AC chung
=>tam giác HCA = Tam giác ACN (c-c-c)
=) góc H= góc N =90 độ
Có CN vuông góc HA vuông góc BM
=> BM//CN
=> MBCN là hình thang mak góc BMN =90 đố => MBCN là hình thang vuông (dpcm)
\(AE\cdot AB=AH^2\)
nên \(\dfrac{AE\cdot AB}{AB^2}=\dfrac{AH^2}{AB^2}\)
\(\Leftrightarrow\dfrac{AE}{AB}=\dfrac{AH^2}{AB^2}\)
\(AF\cdot AC=AH^2\)
\(\Leftrightarrow\dfrac{AF\cdot AC}{AC^2}=\dfrac{AH^2}{AC^2}\)
hay \(\dfrac{AF}{AC}=\dfrac{AH^2}{AC^2}\)
\(\dfrac{AE}{AB}+\dfrac{AF}{AC}=AH^2\left(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\right)=AH^2\cdot\dfrac{BC^2}{AB^2\cdot AC^2}\)
\(=AH^2\cdot\dfrac{BC^2}{\left(AB\cdot AC\right)^2}=AH^2\cdot\dfrac{BC^2}{\left(AH\cdot BC\right)^2}=1\)
:))