Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Tam giác ABC vuông ở A và có góc B ^ = 50 0 ⇒ A C B ^ = 90 0 − 50 0 = 40 0
Vì A C → , C B → = 180 0 − A C B ^ = 180 0 − 40 0 = 140 0 .

Chọn C.
Ta có :
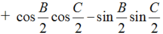
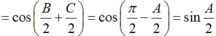 A đúng.
A đúng.
+ tanA + tanB + tanC = tanA.tanB.tanC ⇔ -tanA(1 – tanBtanC) = tanB + tanC
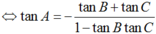 ⇔ tan A = -tan(B + C). B đúng.
⇔ tan A = -tan(B + C). B đúng.
+ cotA + cotB + cotC = cotA.cotB.cotC ⇔ cotA(cotBcotC – 1) = cotB + cotC
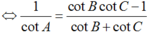 ⇔ tanA = cot(B + C). C sai.
⇔ tanA = cot(B + C). C sai.
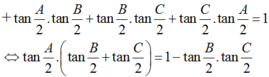
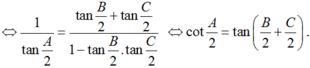 D đúng.
D đúng.

Chọn A.
Từ giả thiết suy ra góc C = 600
Dùng bảng giá trị lượng giác các góc đặc biệt ta có:
![]() ; sin C = 0,5 ; sinB = 0,5.
; sin C = 0,5 ; sinB = 0,5.

Ta có; cosB =cos 30 0 = 3 2 ⇒ sin C = c osB = 3 2
Và sinB =sin 30 0 = 1 2 ⇒ c os C = sinB = 1 2
Chọn A.

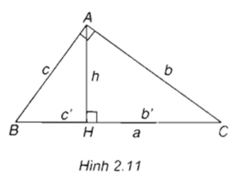
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
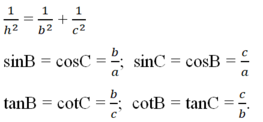

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
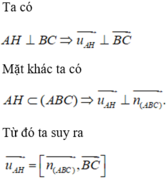
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.

Mệnh đề A sai
Đúng: hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh tương ứng bằng nhau
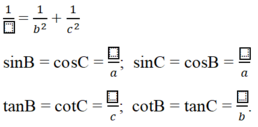
Chọn D.