Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A. \(\sin A = \sin \,(B + C)\)
Ta có: \((\widehat A + \widehat C) + \widehat B= {180^o}\)
\(\Rightarrow \sin \,(B + C) = \sin A\)
=> A đúng.
B. \(\cos A = \cos \,(B + C)\)
Sai vì \(\cos \,(B + C) = - \cos A\)
C. \(\;\cos A > 0\) Không đủ dữ kiện để kết luận.
Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)
Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)
D. \(\sin A\,\, \le 0\)
Ta có \(S = \frac{1}{2}bc.\sin A > 0\). Mà \(b,c > 0\)
\( \Rightarrow \sin A > 0\)
=> D sai.
Chọn A

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
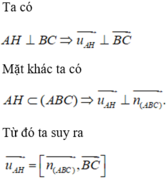
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

\(\widehat{B}=180^o-\left(40^o+120^o\right)=20^o\).
\(AH=AB.sinB=35.sin20^o\cong12cm.\)
\(\widehat{HCA}=180^o-120^o=60^o\).
\(AH=AC.sin60^o\Rightarrow AC=\dfrac{AH}{sin60}=\dfrac{12}{\dfrac{\sqrt{3}}{2}}=8\sqrt{3}\).
Áp dụng định lý Cô-sin:
\(BC=\sqrt{AB^2+AC^2-2.AB.AC.sinA}\)\(=\sqrt{35^2+\left(8\sqrt{3}\right)^2-2.35.8\sqrt{3}.cos40^o}\cong26cm\).
Vậy \(a=26cm;b=8\sqrt{3}cm,\)\(\widehat{B}=20^o\).

Đáp án D
Ta có:
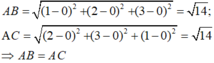
Ta thấy tam giác ABC cân tại đỉnh A. Do đó, AD đồng thời là đường cao của tam giác ABC nên các khẳng định A, B và C đều đúng.
Vậy khẳng định D sai.

Chọn C.
Ta có :
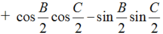
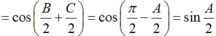 A đúng.
A đúng.
+ tanA + tanB + tanC = tanA.tanB.tanC ⇔ -tanA(1 – tanBtanC) = tanB + tanC
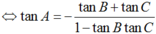 ⇔ tan A = -tan(B + C). B đúng.
⇔ tan A = -tan(B + C). B đúng.
+ cotA + cotB + cotC = cotA.cotB.cotC ⇔ cotA(cotBcotC – 1) = cotB + cotC
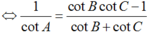 ⇔ tanA = cot(B + C). C sai.
⇔ tanA = cot(B + C). C sai.
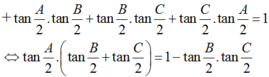
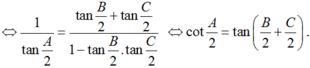 D đúng.
D đúng.


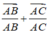
Chọn D.
Tam giác ABC vuông ở A và có góc B ^ = 50 0 ⇒ A C B ^ = 90 0 − 50 0 = 40 0
Vì A C → , C B → = 180 0 − A C B ^ = 180 0 − 40 0 = 140 0 .