Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\le\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
\(\Leftrightarrow2x-3+5x\left(x-2\right)\le5x^2-7\left(2x-3\right)\)
\(\Leftrightarrow2x-3+5x^2-10x< =5x^2-14x+21\)
=>-8x-3<=-14x+21
=>6x<=24
hay x<=4
b: \(\dfrac{6x+1}{18}+\dfrac{x+3}{12}>=\dfrac{5x+3}{6}+\dfrac{12-5x}{9}\)
=>2(6x+1)+3(x+3)>=6(5x+3)+4(12-5x)
=>12x+2+3x+9>=30x+18+48-20x
=>15x+11>=10x+66
=>5x>=55
hay x>=11

Áp dụng bđt Cauchy ta có :
\(x^4+1\ge2\sqrt{x^4}=2x^2\)
Khi đó : \(\frac{x^2}{x^4+1}\le\frac{x^2}{2x^2}=\frac{1}{2}\)
Hay \(B\le\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=\pm1\)

Để x2 - 8x + 12 không âm thì x2 - 8x + 12 ≥ 0
<=> ( x - 2 )( x - 6 ) ≥ 0
Xét hai trường hợp :
1. \(\hept{\begin{cases}x-2\ge0\\x-6\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge2\\x\ge6\end{cases}}\Leftrightarrow x\ge6\)
2. \(\hept{\begin{cases}x-2\le0\\x-6\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le2\\x\le6\end{cases}}\Leftrightarrow x\le2\)
Vậy với \(\orbr{\begin{cases}x\ge6\\x\le2\end{cases}}\)thì x2 - 8x + 12 không âm
Theo bài ra ta có : \(x^2-8x+12\ge0\)
\(\Leftrightarrow\left(x-6\right)\left(x-2\right)\ge0\)
TH1 : \(\hept{\begin{cases}x-6\ge0\\x-2\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge6\\x\ge2\end{cases}\Leftrightarrow}x\ge6}\)
TH2 : \(\hept{\begin{cases}x-6\le0\\x-2\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le6\\x\le2\end{cases}\Leftrightarrow x\le2}}\)
Vậy với giá trị \(x\le2;x\ge6\)thì biểu thức trên ko âm

a) 2x−2=2(x−1)≠02x−2=2(x−1)≠0 khi x−1≠0x−1≠0 hay x≠1x≠1
x2−1=(x−1)(x+1)≠0x2−1=(x−1)(x+1)≠0 khi x−1≠0x−1≠0 và x+1≠0x+1≠0
hay x≠1x≠1 và x≠−1x≠−1
2x+2=2(x+1)≠02x+2=2(x+1)≠0 khi x+1≠0x+1≠0 hay x≠−1x≠−1
Do đó điều kiện để giá trị của biểu thức được xác định là x≠−1,x≠1x≠−1,x≠1
b) Để chứng minh biểu thức không phục thuộc vào biến x ta phải chứng tỏ rằng có thể biến đổi biểu thức này thành một hằng số.
Thật vậy:(x+12x−2+3x2−1−x+32x+2).4x
a, \(2x-2\ne0\) khi \(2x\ne2\Leftrightarrow x\ne1\)
\(x^2-1=\left(x+1\right)\left(x-1\right)\ne0\) khi \(x+1\ne0\) và \(x-1\Leftrightarrow x\ne-1\) và \(x\ne1\)
\(2x+2=2\left(x+1\right)\ne0\) khi \(x\ne-1\)
điều kiên của x để giá trị của biểu thức được xác định là : \(x\ne-1\) và \(x\ne1\)
b, \(\left(\dfrac{x+1}{2x-2}\dfrac{3}{x^2-1}-\dfrac{x+3}{2x+2}\right).\dfrac{4x^2-4}{5}\)
= \(\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x+1\right)\left(x-1\right)}+\dfrac{-\left(x+3\right)}{2\left(x+1\right)}\right].\dfrac{4\left(x^2-1\right)}{5}\)
=\(\dfrac{\left(x+1\right)\left(x+1\right)+3.2-\left(x+3\right)\left(x-1\right)}{2\left(x+1\right)\left(x-1\right)}.\dfrac{4\left(x+1\right)\left(x-1\right)}{5}\)
= \(\dfrac{x^2+2x+1+6-x^2+x-3x+3}{2\left(x+1\right)\left(x-1\right)}.\dfrac{4\left(x+1\right)\left(x-1\right)}{5}\)
= \(\dfrac{10}{2\left(x+1\right)\left(x-1\right)}.\dfrac{4\left(x+1\right)\left(x-1\right)}{5}\)
= \(\dfrac{40\left(x+1\right)\left(x-1\right)}{10\left(x+1\right)\left(x-1\right)}\)
Vậy giá trị biểu thức được xác định thì nó không phụ thuộc vào giá trị của biến X

\(a,A=\frac{x^2+2x}{x\left(x-3\right)}=\frac{x\left(x+2\right)}{x\left(x-3\right)}=\frac{x+2}{x-3}=\frac{x-3+5}{x-3}=1+\frac{5}{x-3}\)
\(b,A< 0< =>1-\frac{5}{x+3}< 0< =>\frac{5}{x+3}>1< =>5>x+3< =>x>2\)
Vậy...........................

1) x(x - 1)(x² + 4) = 0
x = 0 hoặc x - 1 = 0
x = 0 hoặc x = 1
Vậy phương trình đã cho có 2 nghiệm
2) Do x² ≥ 0
⇒x² + 1 > 0
Để biểu thức đã cho nhận giá trị âm thì -x < 0
Hay x > 0


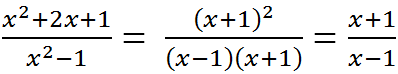
\(x+\dfrac{1}{x-2}=\dfrac{x^2-2x+1}{x-2}=\dfrac{\left(x-1\right)^2}{x-2}\)
Để biểu thức trên không âm hay \(\dfrac{\left(x-1\right)^2}{x-2}\ge0\) thì:
\(\left[{}\begin{matrix}x-2>0\\\left(x-1\right)^2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>2\\x=1\end{matrix}\right.\)