Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Xét ABM và ACM
AB=AC , AM chung , BM=MC(Do M là trung điểm của BC)
ABM = ACM
BAM = CAM (1)
Mà AM nằm giữa AB và AC ( Do M nằm giữa B và C) (2)
Từ (1) và (2)
AM là tia phân giác của BAC
b,Xét BNC và DNC
NC chung , CB = CD
Góc BCN = DCN
Tam giác:BNC = DNC
Góc BNC = DCN
Mà BNC + DCN = 180
BNC = 90
CN vuông góc với BD

Sửa đề: M là trung điểm của BC
a: ΔABC cân tại A có AM là trung tuyến
nên AM là phân giác của góc BAC
b: Xét ΔABC có
AM,BD,CE là các đường phân giác
=>AM,BD,CE đồng quy tại H

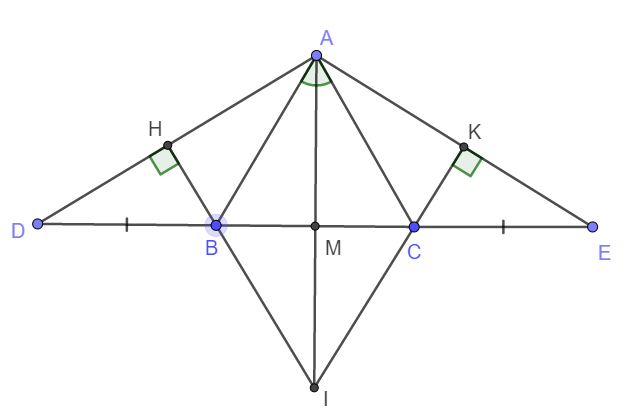
a) Do tam giác ABC cân tại A nên AB = AC; \(\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ABD và ACE có:
DB = EC
AB = AC
\(\widehat{ABD}=\widehat{ACE}\)
\(\Rightarrow\Delta ABD=\Delta ACE\left(c-g-c\right)\)
b) Do \(\Delta ABD=\Delta ACE\Rightarrow\widehat{ADB}=\widehat{AEC}\) và AD = AE
Suy ra \(\Delta DHB=\Delta EKC\) (Cạnh huyền - góc nhọn)
\(\Rightarrow DH=EK\Rightarrow AH=AK\)
c) Xét tam giác vuông AHI và AKI có:
AH = AK
Cạnh AI chung
\(\Rightarrow\Delta AHI=\Delta AKI\) (Cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{HAI}=\widehat{KAI}\) hay I là phân giác của gocsc DAE.
d) Xét tam giác cân ABC có AM là trung tuyến nên đồng thời là đường cao.
Xét tam giác cân ADE có AM là đường cao đồng thời phân giác.
Vậy nên A, M, I thẳng hàng. Suy ra AM, HB, KC đồng quy tại điểm I.
e) Ta có BM = MC và \(IM\perp BC\) nên IM là trung trực của BC
Suy ra IB = IC hay IC là tam giác BIC cân tại I.
f) Tam giác ABC cân có góc A = 60o nên ABC là tam giác đều.
Xét tam giác DAC có AB = DB = BC nên nó là tam giác vuông tại A.
Suy ra AC // HI
\(\Rightarrow\widehat{CBI}=\widehat{BCA}=60^o\)
Tam giác cân BIC có một góc bằng 60o nên nó là tam giác đều.

a) Chứng minh được ∆ A M B = ∆ A M C (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC.
b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.