moi nguoi giup minh bai nay nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2022
a: Xét tứ giác AECF có
AF//EC
AF=EC
Do đó: AECF là hình bình hành
b: Xét tứ giác ABEF có
AF//BE
AF=BE
Do đó: ABEF là hình bình hành
mà AF=AB
nên ABEF là hình thoi
Suy ra: AE\(\perp\)BF
c: \(\widehat{ABD}=180^0-60^0=120^0\)
e: Xét tứ giác FDCE có
FD//CE
FD=CE
Do đó: FDCE là hình bình hành
ma FD=CD
nên FDCE là hình thoi
=>FC là đường trung trực của DE
hay E và D đối xứng nhau qua FC
giup minh voi bai 4 nha
NT
sua lai anh roi nhe minh rat mong moi nguoi giup do
1
KN
4 tháng 7 2017
a/ Theo bài ra: \(x^2+y^2=6;xy=1\)
=> \(x^2+y^2+2xy=8\)
=> \(\left(x+y\right)^2=8\)
=> \(x+y=\sqrt{8}\)
b/ Theo bài ra: \(x^2+y^2=14;xy=1\)
=>\(x^2+y^2-2xy=12\)
=> \(\left(x-y\right)^2=12\)
=> \(x-y=\sqrt{12}\)
c/ Theo bài ra: \(a^2+b^2=116;ab=40\)
=> \(\left(a^2+b^2\right)^2=116^2;a^2b^2=1600\)
=> \(a^4+b^4+2a^2b^2=116^2\)
=> \(a^4-2a^2b^2+b^4+4a^2b^2=13456\)
=> \(a^4-2a^2b^2+b^4=7056\)
14 tháng 10 2017
Bài 2 nhìn tổng quát thì tahays tiwur A đến K đều dung hđt số 3
còn L thì đặt dyas âm trước 3 hạng tử đầu dung hđt 1 rồi áp dụng hđt 3
m tương tự đặt dấu âm làm nhân tử chung 3 hạng tử sau rồi áp dụng hđt số 2 sung hđt số 3
.hết
TN
24 tháng 8 2017
Bài 1:
\(A=3-x^2\)
Với mọi giá trị của x ta có:
\(x^2\ge0\Rightarrow3-x^2\le3\)
Vậy MAx A = 3
Để A = 3 thì \(x=0\)
\(B=4x-x^2+3=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7\)
Với mọi giá trị của x ta có:
\(\left(x-2\right)^2\ge0\Rightarrow-\left(x-2\right)^2\le0\)
\(\Rightarrow-\left(x-2\right)^2+7\le7\)
Vậy Max B = 7
Để B = 7 thì \(x-2=0\Rightarrow x=2\)
\(C=x-x^2=-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\)
Với mọi giá trị của x ta có:
\(\left(x-\dfrac{1}{2}\right)^2\ge0\Rightarrow-\left(x-\dfrac{1}{2}\right)^2\le0\)
\(\Rightarrow-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
Vậy Max C = \(\dfrac{1}{4}\)
Để C = \(\dfrac{1}{4}\) thì \(x-\dfrac{1}{2}=0\Rightarrow x=\dfrac{1}{2}\)
\(D=\dfrac{1}{x^2+2x+3}=\dfrac{1}{\left(x+1\right)^2+2}\)
Với mọi giá trị của x ta có:
\(\left(x+1\right)^2\ge0\Rightarrow\left(x+1\right)^2+2\ge2\)
\(\Rightarrow\dfrac{1}{\left(x+1\right)^2+2}\le\dfrac{1}{2}\)
Vậy Max D= \(\dfrac{1}{2}\)
Để \(D=\dfrac{1}{2}\) thì \(x+1=0\Rightarrow x=-1\)
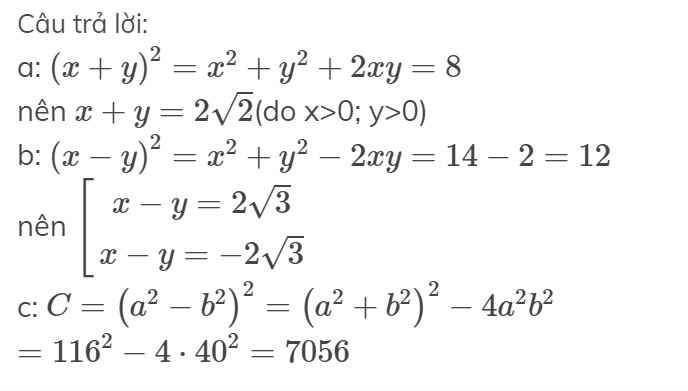
Giúp e với mọi nguoi oi kt 15'
\(\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+...+\frac{2014}{2015!}\)
\(=\frac{2}{2!}-\frac{1}{2!}+\frac{3}{3!}-\frac{1}{3!}+\frac{4}{4!}-\frac{1}{4!}+...+\frac{2015}{2015!}-\frac{1}{2015!}\)
\(=1-\frac{1}{2!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{3!}-\frac{1}{4!}+...+\frac{1}{2014!}-\frac{1}{2015!}\)
\(=1-\frac{1}{2015!}< 1\left(đpcm\right)\)