Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

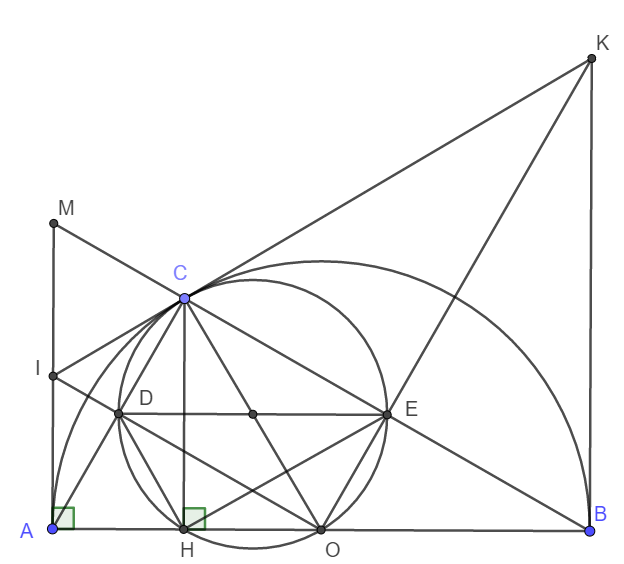
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.

Ngủ đi , bây giờ chẳng bạn nào giải đâu !!!
Chúc học giỏi !!!
A B C I O M S H Q N D E F K J T
a) Gọi S là điểm chính giữa của cung nhỏ BC. Do dây BC cố định nên điểm S cũng cố định. Ta đi chứng minh tiếp tuyến tại M của (MKO) luôn đi qua S.
Do S là điểm chính giữa cung nhỏ BC của (O) => SB=SC và A,I,S thẳng hàng (Vì AI là phân giác của ^BAC nội tiếp chắn cung BC)
Ta có: ^SIB là góc ngoài \(\Delta\)AIB => ^SIB = ^IBA + ^IAB = 1/2(^BAC + ^ABC)
Mà ^SBI = ^IBC + ^SBC = 1/2(^ABC + ^CAS) = 1/2(^ABC + ^BAC) nên ^SIB = ^SBI => \(\Delta\)BSI cân tại S
=> SB=SI => SB=SC=SI => S là tâm của (BIC). Ta thấy M nằm trên (BIC) nên SM = SI (1)
Dễ thấy 3 điểm S,K,O thẳng hàng (Cùng nằm trên trung trực của BC) => SKO là cắt tuyến của (OIK)
Xét đường tròn (OIK): Cát tuyến SKO, tiếp tuyến SI => SI2 = SK.SO (Hệ thức lượng trong đường tròn) (2)
Từ (1) và (2) => SM2 = SK.SO => \(\Delta\)SMK ~ \(\Delta\)SOM (c.g.c)
=> ^SMK = ^SOM = 1/2.Sđ(MK của đường tròn (MKO) => MS là tiếp tuyến của đường tròn (MKO)
Hay tiếp tuyến tại M của (MKO) luôn đi qua S cố định (đpcm).
b) Ta có: Tứ giác SIOQ nội tiếp có góc ngoài là ^AIO => ^OQS = ^AIO (*)
Theo câu a: SI2 = SK.SO => SB2 = SK.SO = SK.R (3)
Kẻ đường kính SN của đường tròn (O), BC cắt OS tại T => ^SBN = 900
=> \(\Delta\)SBN vuông tại B có đường cao BT => SB2 = ST.SN (Hệ thức lượng). Hay SB2 = ST.2R (4)
Từ (3) và (4) => SK=2.ST => T là trung điểm của SK. Tứ đó: S và K đối xứng với nhau qua BC
Mà I và H cũng đối xứng nhau qua BC nên tứ giác IKSH là hình thang cân
^OSQ = ^IHS = ^IKO =^AIO (=1/2.Sđ(OI của (IKO) ) => ^OSQ = ^AIO (**)
Từ (*) và (**) suy ra: ^OQS = ^OSQ => \(\Delta\)SOQ cân tại O => OS = OQ = R => Q thuộc (O) (đpcm).
c) Xét tứ giác SIOQ nội tiếp đường tròn có: ^OIQ = ^OSQ (Góc nội tiếp cùng chắn cung OQ)
Lại có: ^OSQ = ^AIO (cmt) nên ^OIQ = ^AIO => IO là tia phân giác của ^AIQ
Dễ dàng chỉ ra được: IA=IQ (Gợi ý: Hạ OX và OY vuông góc với IA và IQ) => \(\Delta\)AIQ cân tại I
Xét \(\Delta\)AIQ: Cân đỉnh I, tia phân giác IO (cmt) => IO đồng thời là đường cao => IO vuông góc AQ (đpcm).
d) Gọi J là giao điểm của AS với BC, E và F lần lượt là hình chiếu của O lên AC,AB. Đặt AB=c, BC=a, CA=b
Ta có: \(\Delta\)AJC ~ \(\Delta\)ABS (g.g) => AJ.AS = c.b (5)
\(\Delta\)SJB ~ \(\Delta\)SBA (g.g) => SB2 = SJ.AS (6)
Từ (5) và (6) suy ra: c.b + SB2 = AJ.AS + SJ.AS = AS2 < SN2 = 4R2 (Quan hệ giữa đường kính và dây cung)
\(\Rightarrow bc+BT^2+ST^2\le4R^2\)(ĐL Pytagore) \(\Rightarrow bc+\frac{a^2}{4}+\left(R-OT\right)^2\le4R^2\)
\(\Rightarrow bc+\frac{a^2}{4}+R^2-2R.OT+OT^2\le4R^2\)\(\Leftrightarrow bc+\frac{a^2}{4}-2R.OT+OT^2\le3R^2\)
Tương tự: \(ab+\frac{c^2}{4}-2R.OF+OF^2\le3R^2;\)\(ca+\frac{b^2}{4}-2R.OE+OE^2\le3R^2\)
Do đó: \(ab+bc+ca+\frac{a^2+b^2+c^2}{4}-2R\left(OT+OE+OF\right)+OT^2+OE^2+OF^2\le9R^2\)
Áp dụng BĐT: \(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}\) và \(a^2+b^2+c^2\ge ab+bc+ca\) ta có:
\(ab+bc+ca+\frac{ab+bc+ca}{4}-2R\left(OT+OE+OF\right)+\frac{\left(OT+OE+OF\right)^2}{3}\le9R^2\)
\(\Leftrightarrow\frac{5\left(ab+bc+ca\right)}{4}-2R\left(OT+OE+OF\right)+\frac{\left(OT+OE+OF\right)^2}{3}\le9R^2\)
Áp dụng ĐL Carnot cho \(\Delta\)ABC có tâm ngoại tiếp O: \(OT+OE+OF=R+r\)
Từ đó có: \(\frac{5\left(ab+bc+ca\right)}{4}-2R\left(R+r\right)+\frac{\left(R+r\right)^2}{3}\le9R^2\)
\(\Leftrightarrow\frac{5\left(ab+bc+ca\right)}{4}\le9R^2+2R\left(R+r\right)-\frac{\left(R+r\right)^2}{3}\)
\(\Leftrightarrow\frac{5\left(ab+bc+ca\right)}{4}\le\frac{32R^2+4Rr-r^2}{3}=\frac{\left(4R+r\right)\left(8R-r\right)}{3}\)
\(\Rightarrow ab+bc+ca\le\frac{4\left(4R+r\right)\left(8R-r\right)}{15}\)
Hay \(AB.BC+BC.CA+CA.AB\le\frac{4\left(4R+r\right)\left(8R-r\right)}{15}\) (đpcm).