Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B E F x y M K O
a)\(\hept{\begin{cases}Ax⊥AB\\By⊥AB\end{cases}}\)=> Ax // By.\(\Delta KFB\)có EA // FB nên\(\frac{KF}{KA}=\frac{BF}{AE}\)(hệ quả định lí Ta-lét) mà EA = EM ; FM = FB (tính chất của 2 tiếp tuyến)
\(\Rightarrow\Delta AEF\)có\(\frac{KF}{KA}=\frac{MF}{ME}\)nên MK // AE (định lí Ta-lét đảo) mà\(AE⊥AB\Rightarrow MK⊥AB\)
b)\(\widehat{EOM}=\frac{\widehat{AOM}}{2};\widehat{FOM}=\frac{\widehat{MOB}}{2}\)(tính chất 2 tiếp tuyến) mà\(\widehat{EOM}+\widehat{FOM}=180^0\)(kề bù)
\(\Rightarrow\widehat{EOF}=\widehat{EOM}+\widehat{FOM}=\frac{180^0}{2}=90^0\)
\(\Rightarrow\Delta EOF\)vuông tại O có OE + OF > EF (bđt tam giác) ; OE + OF < 2EF (vì OE,OF < EF)
\(\Rightarrow1< \frac{OE+OF}{EF}< 2\Rightarrow2< \frac{P_{EOF}}{EF}< 3\Rightarrow\frac{1}{3}< \frac{EF}{P_{EOF}}< \frac{1}{2}\)(1)
Hình thang AEFB (AE // FB) có diện tích là :\(\frac{\left(AE+FB\right).AB}{2}=\frac{\left(EM+FM\right).2R}{2}=EF.R\)
SAEO = SMEO vì có đáy OA = OM ; đường cao AE = ME\(\Rightarrow S_{MEO}=\frac{1}{2}S_{AEMO}\)
SFOM = SFOB vì có đáy FM = FB ; đường cao OM = OB\(\Rightarrow S_{FOM}=\frac{1}{2}S_{MFBO}\)
\(\Rightarrow S_{EOF}=\frac{1}{2}\left(S_{AEMO}+S_{MFBO}\right)=\frac{EF.R}{2}\).Từ tâm đường tròn nội tiếp I của\(\Delta EOF\)kẻ các đường vuông góc với OE,OF,EF thì\(S_{EOF}=S_{EIF}+S_{EIO}+S_{OIF}\)\(\Leftrightarrow\frac{EF.R}{2}=\frac{EF.r+EO.r+OF.r}{2}\)
\(\Rightarrow EF.R=P_{EOF}.r\Rightarrow\frac{r}{R}=\frac{EF}{P_{EOF}}\)(2).Thay (2) vào (1) ta có đpcm.

a) Xét tứ giác AOMC có
ˆCAOCAO^ và ˆCMOCMO^ là hai góc đối
ˆCAO+ˆCMO=1800(900+900=1800)CAO^+CMO^=1800(900+900=1800)
Do đó: AOMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Ta có: AOMC là tứ giác nội tiếp(cmt)
nên ˆMAO=ˆOCMMAO^=OCM^(hai góc cùng nhìn cạnh OM)
hay ˆMAB=ˆOCDMAB^=OCD^
Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(Gt)
CA là tiếp tuyến có A là tiếp điểm(Gt)
Do đó: OC là tia phân giác của ˆAOMAOM^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆAOM=2⋅ˆCOM⇔AOM^=2⋅COM^
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OD là tia phân giác của ˆMOBMOB^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆBOM=2⋅ˆMOD⇔BOM^=2⋅MOD^
Ta có: ˆAOM+ˆBOM=1800AOM^+BOM^=1800(hai góc kề bù)
mà ˆAOM=2⋅ˆCOMAOM^=2⋅COM^(cmt)
và ˆBOM=2⋅ˆMODBOM^=2⋅MOD^(cmt)
nên 2⋅ˆCOM+2⋅ˆMOD=18002⋅COM^+2⋅MOD^=1800
⇔ˆCOM+ˆMOD=900⇔COM^+MOD^=900
mà ˆCOM+ˆMOD=ˆCODCOM^+MOD^=COD^(tia OM nằm giữa hai tia OC,OD)
nên ˆCOD=900COD^=900
Xét ΔCOD có ˆCOD=900COD^=900(cmt)
nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)
Xét (O) có
ΔMAB nội tiếp đường tròn(M,A,B∈(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
Xét ΔAMB vuông tại M và ΔCOD vuông tại O có
ˆMAB=ˆOCDMAB^=OCD^(cmt)
Do đó: ΔAMB∼ΔCOD(g-g)
⇔AMCO=BMDOAMCO=BMDO(Các cặp cạnh tương ứng tỉ lệ)
hay AM⋅OD=BM⋅OCAM⋅OD=BM⋅OC(đpcm)

(Quá lực!!!)
E N A B C D O H L
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)

a) Chứng minh tứ giác OBDF nội tiếp.
Định tâm I đường tròn ngoại tiếp tứ OBDF.
Ta có: DBO = 900 và DFO = 900(tính chất tiếp tuyến)
Tứ giác OBDF có DBO+DFO =1800 nên nội tiếp được trong một đường tròn.
Tâm I đường tròn ngoại tiếp tứ giác OBDF là trung điểm của OD
b) Tính Cos DAB .
Áp dụng định lí Pi-ta-go cho tam giác OFA vuông ở F ta được:
\(OA=\sqrt{OF^2+AF^2}=\sqrt{R^2+\left(\frac{4R}{3}\right)}=\frac{5R}{3}\)
\(COS\)\(FAO=\frac{AF}{OA}=\frac{4R}{3}:\frac{5R}{3}=0,8=>COSDAB=0,8\)
c) Kẻ OM ⊥ BC ( M ∈ AD) . Chứng minh \(\frac{BD}{DM}-\frac{DM}{AM}\) =1
∗ OM // BD ( cùng vuông góc BC) ⇒ MOD BDO = (so le trong) và BDO ODM = (tính chất hai tiếp tuyến cắt nhau)
Suy ra: MDO =MOD.
Vậy tam giác MDO cân ở M. Do đó: MD = MO
∗ Áp dụng hệ quả định lí Ta let vào tam giác ABD có OM // BD ta được:
\(\frac{BD}{OM}=\frac{AD}{AM}HAY\frac{BD}{DM}=\frac{AD}{AM}\)(VÌ MD=MO)
\(=>\frac{BD}{DM}=\frac{AM+DM}{AM}=1+\frac{DM}{AM}\)
Do đó:\(\frac{DM}{BM}-\frac{DM}{AM}=1\left(đpcm\right)\)
d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R.
∗Áp dụng hệ thức lượng cho tam giác OAM vuông ở O có OF ⊥ AM ta được:
OF2 = MF. AF hay R2 = MF. \(\frac{4r}{3}\)⇒ MF = \(\frac{3r}{4}\)
∗ Áp dụng định lí pi ta go cho tam giác MFO vuông tại F ta được:
OM = \(\sqrt{OF^2+MF^2}=\sqrt{R^2+\frac{3R}{4}^2}=\frac{5R}{4}\)
∗ OM //BD =>\(\frac{OM}{BD}=\frac{AO}{AB}=>BD=\frac{OM.AB}{OA}=\frac{5R}{4}.\left(\frac{5R}{3}+R\right):\frac{5R}{3}=2R\)
Gọi S là diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O)
S1 là diện tích hình thang OBDM.
S2 là diện tích hình quạt góc ở tâm BON = 90 0
Ta có: S = S1 – S2 .
\(S1=\frac{1}{2}\left(OM+BD\right).OB=\frac{1}{2}\left(\frac{5R}{4}+2R\right).R=\frac{13R^2}{8}\left(đvdt\right)\)
\(S2=\frac{\pi R^2.90^0}{360^0}=\frac{\pi R^2}{4}\left(đvdt\right)\)
Vậys=s1-s2=\(\frac{13r^2}{8}-\frac{\pi r^2}{4}=\frac{r^2}{8}\left(13-2\pi\right)\left(đvdt\right)\)

Giải:
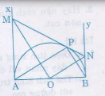
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3
 Phạm Cao Thúy An: Biết rồi còn hỏi làm gì?
Phạm Cao Thúy An: Biết rồi còn hỏi làm gì?
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.