Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMCD và ΔMEC có
góc MCD=góc MEC
góc CMD chung
=>ΔMCD đồng dạng với ΔMEC
b: Xét (O) có
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại K
ΔMCO vuông tại C có CK là đường cao
nên MK*MO=MC^2
c: góc AOC=2*góc AIC=120 độ
=>góc AOM=góc COM=60 độ
Xét ΔCOM vuông tại C có tan COM=CM/CO
=>CM/R=căn 3
=>CM=R*căn 3

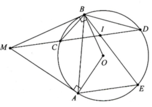
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')