Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cảm ơn em câu hỏi của em thật là thù vị. Về thắc mắc của em cô nghĩ chắc cũng có nhiều bạn đang muốn biết lắm ý nhỉ? Về vấn đề em hỏi cô xin trả lời như sau:
Tình theo a ở đây không phải là a mà mình tùy chọn em nhá. a ở đây là một ẩn a, em cứ tính độ dài của tam giác đó theo ẩn a thôi em ạ!
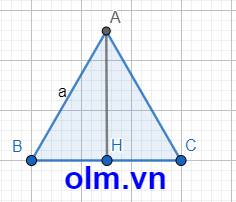
Vì ABC là tam giác đều nên đường cao cũng là đường trung tuyến của tam giác. Gọi AH là đường cao của tam giác thì
BH = HC = \(\dfrac{1}{2}\)a
Xét tam giác ACH vuông tại H. Theo pytago ta có:
AC2 = AH2 + HC2
⇒ AH2 = AC2 - HC2
⇒AH2 = a2 - (\(\dfrac{1}{2}\)a)2 = \(\dfrac{3}{4}\)a2
⇒ AH = \(\sqrt{\dfrac{3}{4}a^2}\) = \(\dfrac{3\sqrt{a}}{2}\)

Bài 1:
Chiều dài là 26x9/13=18(m)
Chiều rộng là 26-18=8(m)
Diện tích là 18x8=144(m2)

a) A là phân giác \(\widehat{BAC}\)\(\Rightarrow\frac{DC}{DB}=\frac{AC}{AB}=\frac{16}{12}=\frac{4}{3}\Rightarrow\frac{DC+DB}{DB}=\frac{4+3}{3}=\frac{7}{3}\Rightarrow\frac{BD}{DB}=\frac{7}{3}\)
\(\Rightarrow DB=\frac{3}{7}BC=\frac{60}{7}\left(cm\right)\) và \(\Rightarrow DC=\frac{80}{7}\left(cm\right)\)
Kẻ DE vuông góc với AC và DE vuông góc với AC ; AB vuông góc với AC => DE//AB
Áp dụng định lí Ta-let có: \(\frac{DE}{AB}=\frac{CD}{CB}=\frac{\frac{80}{7}}{20}=\frac{4}{7}\Rightarrow DE=\frac{4}{7}AB=\frac{48}{7}\left(cm\right)\)
SACD=\(\frac{1}{2}DE.AC=\frac{1}{2}\cdot\frac{48}{7}.16=\frac{384}{7}cm^2\)
SABD=SABC-SACD\(=\frac{1}{2}.AC.AB-\frac{384}{7}=\frac{288}{7}\left(cm^2\right)\)
Tỉ lệ diện tích ABD và diện tích ACD là \(\frac{3}{4}\)
b) Từ A kẻ đường cao AH ( H thuộc BC).
Do tam giác ABC vuông tại A
Áp dụng định lí pi-ta-go có:
\(BC\sqrt{AB^2+AC^2}=20cm\)
c) Áp dụng định lý cosin trong tam giác ABD và ADC ta lần lượt có đẳng thức:
\(BD^2=AB^2+AD^2-2.AB.AD.cos\left(45\right)\)
\(DC^2=AC^2+AD^2-2.AC.AD.cos\left(\text{45}\right)\left(2\right)\)
Trừ vế với vế có:\(BD^2-DC^2=AB^2-AC^2-2.AB.AD.cos\left(45\right)+2.AC.AD.cos\left(45\right)\)
\(\left(BD-DC\right)^2-DC^2=-122+4.\sqrt{\left(2\right)}.AD\)
\(400-40.DC=-122+....\)
\(\Rightarrow128-10.DC=\sqrt{\left(2\right)}.AD\left(3\right)\)
Thay (3) v ào (2): Tính được DC = \(\frac{80}{7}\) cm;
\(BD=BC-Dc=\frac{60}{7}\left(cm\right)\)
d) Có SABC= \(AB\cdot\frac{AC}{2}=AH\cdot\frac{BC}{2}\)
Suy ra: \(AH=AB\cdot\frac{AC}{BC}=12\cdot\frac{16}{20}=9,6\left(cm\right)\)
a) Độ dài đường cao \(h\):
\(SinB=\dfrac{h}{AB}\Rightarrow h=AB.sin60^o=\dfrac{a\sqrt[]{2}}{2}\left(cm\right)\)
b) Nửa chu vi tam giác đó :
\(p=\dfrac{a+a+a}{2}=\dfrac{3a}{2}\)
Diện tích tam giác :
\(S=\sqrt[]{p\left(p-a\right)\left(p-a\right)\left(p-a\right)}\)
\(\Rightarrow S=\sqrt[]{p\left(p-a\right)^3}\)
\(\Rightarrow S=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{3a}{2}-a\right)^3}=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{a}{2}\right)^3}=\sqrt[]{\dfrac{3a^4}{16}}=\dfrac{a^2\sqrt[]{3}}{4}\)
a:Gọi tam giác đề bài cho là ΔABC đều có AH là đường cao
=>H là trung điểm của BC
=>HB=HC=a/2
AH=căn AB^2-AH^2
=a*căn 3/2
b: S ABC=1/2*AH*BC
=a^2*căn 3/4