K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SV
Sinh Viên NEU
CTVVIP
13 tháng 11 2023
Bạn có thể liên lạc với các giáo viên olm để nhờ tư vấn cách dùng nha
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 11 2023
Olm chào bạn. Cảm ơn bạn đã tin tưởng và sử dụng nền tảng giáo dục trực tuyến olm. Bạn liên hệ với mình qua zalo để được hỗ trợ nhanh nhất nhé. Thương Hoài 0385168017. Trân trọng!
DD
Ai có acc bangbang vip 12 tank trở lên cần người cày không tui cày cho, tất cả các sever đều cày hết
4
CM
14 tháng 11 2019
Xem lô đất có 4 vị trí gồm 2 vị trí 1 nền,1 vị trí 2 nền và 1 vị trí 3 nền
Bước 1: nhóm thứ nhất chọn 1 vị trí cho 2 nền có 4 cách và mỗi cách có 2! = 2 cách chọn nền cho mỗi người. Suy ra có 4 . 2 = 8 cách chọn nền
Bước 2 nhóm thứ hai chọn 1 trong 3 vị trí còn lại cho 3 nền có 3 cách và mỗi cách có 3! = 6 cách chọn nền cho mỗi người. Suy ra có 3 . 6 = 18cách chọn nền
Vậy có 8 . 18 = 144 cách chọn nền cho mỗi người
Đáp án D
CM
5 tháng 1 2020
Đáp án B
Ta xét bài toán tổng quát n tem thư được dán vào n bì thư sao cho có ít nhất 1 bì thư được dán vào tem thư có số trùng với số của bì thư đó
Đánh số các tem thư là T 1 , T 2 ,.., T n và các bì thư B 1 , B 2 ,…, B n . Bài toán được giải quyết bằng nguyên lý phần bù. Lấy hoán vị n phần tử trừ đi trường hợp xếp mà không có tem thư nào được dán cùng số với bì thư.
+ Để giải quyết bài toán không có tem thư nào được dán cùng số với bì thư. Ta xây dựng dãy số f(n) như sau:
Công việc dán n tem thư vào n bì thư sao cho không có bì thư nào được dán vào tem thư có số trùng với số của bì thư đó. Công việc này gồm có 2 bước sau
- Bước 1: dán tem T1 lên 1 bì thư Bj khác B1, có n – 1 cách
- Bước 2: Dán tem thư Tj vào bì thư nào đó, có 2 trường hợp xảy ra như sau:
+ TH1: Tem thư Tj được dán vào bì thư B1. Khi đó còn lại n – 2 tem (khác T1 và Tj) là T2,…,Tj-1, Tj+1,…,Tn phải dán vào n – 2 bì thư (khác B1 và Bj). Quy trình được lặp lại giống như trên. Nên TH này có số cách dán bằng f(n-2)
+ TH2: tem thư Tj không được dán vào bì thư B1
Khi đó các tem là T2,…,Tj-1, Tj, Tj+1,…,Tn sẽ được đem dán vào các bì B1, B2,…,Bj-1, Bj+1,…,Bn (mà tem thư Tj không được dán vào bì thư B1). Thì Tj lúc này bản chất giống như T1, ta đánh số lại Tj º T1. Nghĩa là n – 1 tem T2, …, Tj-1, T1, Tj+1,…,Tn sẽ được đem dán vào n – 1 bì B1, B2,…,Bj-1,Bj+1,…,Bn với việc đánh số giống nhau. Công việc này lại được lập lại như từ ban đầu.
Nên TH này có số cách dán bằng f (n-1)
+ Ta xét dãy u n = f n như sau
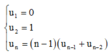
Như vậy kết quả của bài toán: n tem thư được dán vào n bì thư sao cho có ít nhất 1 bì thư được dán vào tem thư có số trùng với số của bì thư đó sẽ là P n - u n
Áp dụng với n = 8, ta được kết quả là 8!-14833=25487.
CM
11 tháng 5 2018
Đáp án A.
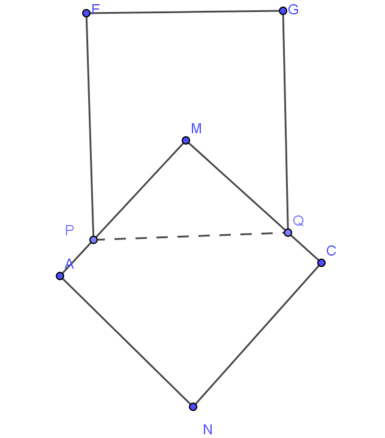
Gọi V 1 là thể tích khối trong xoay khi xoay hình vuông EGQP quanh MN. Khối này có bán kính đáy R = 1 2 E G = 5 2 và đường cao = EP = 5 => V 1 = 5 . 5 2 2 π = 125 4 π
Gọi V 2 là thể tích khối tròn xoay khi xoay hình vuông AMCN quanh MN, khối này là hợp lại của 2 khối nón đêu có bán kính đáy R = 1 2 A C = 5 2 2 Đường cao h = 1 2 M N = 5 2 2 => V 2 = 2 . 1 3 . 5 2 2 . 5 2 2 2 π = 125 2 6 π
Gọi V 3 là thể tích của khối nón tròn xoay khi quay MPQ quanh MN, khối này óc bán kính đáy R = 1 2 P Q = 5 2 đường cao h = d ( M ; P Q ) = 5 2 => V 3 = 1 3 . 5 2 . 5 2 2 . π = 125 12 π
Ta có thể tích của toàn khối tròn xoay V = V 1 + V 2 - V 3 = 125 1 + 2 π 6
PT
6 tháng 4 2016
Gọi a là giá bán
b là giá mua
Lúc đầu bán 1 tấm vải lãi \(\frac{1}{5}\)giá mua nên ta có: \(b=a+\frac{1}{5}b\) <=> a=\(\frac{4}{5}\)b(1)
Nâng giá bán lên 40000đ nữa thì lãi bằng \(\frac{1}{5}\) giá bán nên ta có: \(b=a+40000+\frac{1}{5}a\)
<=> b = \(\frac{6}{5}a\) +40000 (2)
Thế (1) vào (2) ta được: b = \(\frac{24}{25}b\) +40000
<=> \(\frac{1}{25}b=40000\)
<=> b=1 000 000
Vậy giá mua là 1 000 000đ => chọn C
6 tháng 4 2016
CÁCH NÀY CÓ LẼ HIỂU HƠN
Nếu đúng vậy thì bán như ban đầu tiền lãi = 1/6 tiền bán (vốn = 5 phần lãi 1 phần nữa thì tiền bán = 6 phần)
Nếu bán cao them 40000 đồng thì tiền lãi bằng 1/5 tiền bán.
vậy phân số chỉ 40 000 đồng:
1/6 - 1/7 = 1/42 tiền bán
=> tiền bán tấm vải :
40000: 1/42= 1 680 000 đồng
bán tấm vải 1 680 000 lãi 1/5 giá mua tức là 6/5 giá mua là 1 680 000 đồng
=> giá mua tấm vải:
1 680 000:6/5 = 1 400 000 đồng
có