Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

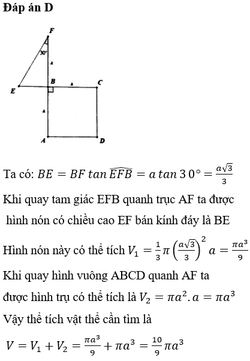
Đáp án B
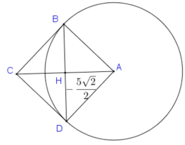
Ta có thể tích vật thể tròn xoay được tạo ra S = S 1 + S 2 .
S 1 = π − 5 2 2 5 25 − x 2 2 d x = 500 π 3 .
S 2 = 1 3 π 5 2 2 3 = π .125.2 2 3.8 = 125 π 2 6
Vậy S = 1000 π + 125 π 2 6 .

Đáp án D.
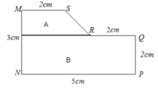
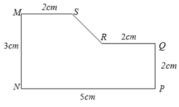
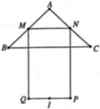
Quay hình A quanh MN thu được khối nón cụt. Quay hình B quanh MN thu được khối trụ
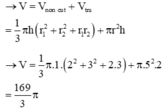

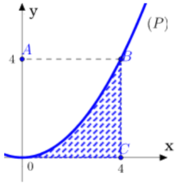
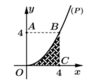
Thể tích vật thể khi quay hình vuông OABC quanh trục Ox là ![]()
Thể tích vật thể khi quay phần gạch sọc quanh Ox là 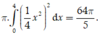
Vậy thể tích vật thể tròn xoay cần tính bằng 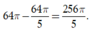
Chọn D.

Phương pháp:
Công thức tính thể tích của khối trụ có bán kính đáy R và chiều cao h: V = π R 2 h
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
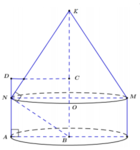
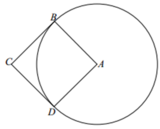
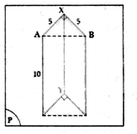
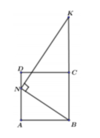
Khi quay tứ giác ANKB quanh trục BK ta được hình trụ có bán kính đáy AB, chiều cao AN và hình nón có bán kính đáy AB, chiều cao K O = B K − A N
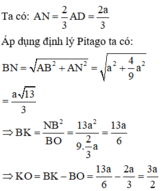
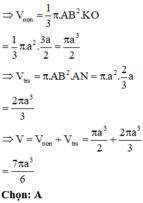




Đáp án A.
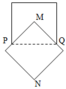
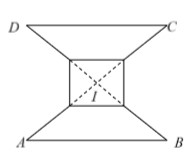
Gọi V 1 là thể tích khối trong xoay khi xoay hình vuông EGQP quanh MN. Khối này có bán kính đáy R = 1 2 E G = 5 2 và đường cao = EP = 5 => V 1 = 5 . 5 2 2 π = 125 4 π
Gọi V 2 là thể tích khối tròn xoay khi xoay hình vuông AMCN quanh MN, khối này là hợp lại của 2 khối nón đêu có bán kính đáy R = 1 2 A C = 5 2 2 Đường cao h = 1 2 M N = 5 2 2 => V 2 = 2 . 1 3 . 5 2 2 . 5 2 2 2 π = 125 2 6 π
Gọi V 3 là thể tích của khối nón tròn xoay khi quay MPQ quanh MN, khối này óc bán kính đáy R = 1 2 P Q = 5 2 đường cao h = d ( M ; P Q ) = 5 2 => V 3 = 1 3 . 5 2 . 5 2 2 . π = 125 12 π
Ta có thể tích của toàn khối tròn xoay V = V 1 + V 2 - V 3 = 125 1 + 2 π 6