Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
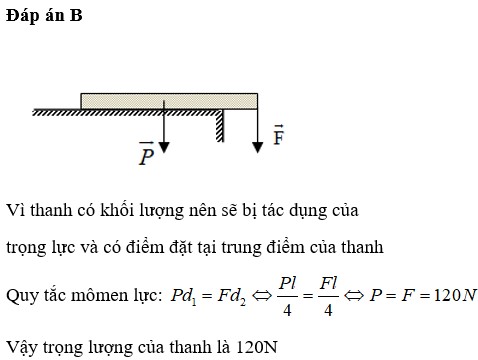
Coi mép bàn là trục quay O, ta có M F = M P
Pl/4 = Fl/4 ⇒ F = P = 40(N)
Chọn B.
Trục quay tại O.
Theo điều kiện cân bằng thì MP/(O) = MF/(O)
→ F.OB = P.OG ↔ F.AB/4=P.AB/4 → P = F = 40 N.
Chọn B.
Trục quay tại O.
Theo điều kiện cân bằng thì M P O = M F O
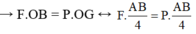
→ P = F = 40 N.
xét tam giác vuông \(ABC\)
ta có : \(AC=\sqrt{10^2-6^2}=\sqrt{64}=8\left(m\right)\)
vì thanh đồng chất tiếp diện đều nên ta có tâm \(G\) là trung điểm \(AB\)
xét tam giác vuông \(AGH\)
ta có : \(AH=AG.cos\widehat{GAH}=5.\dfrac{8}{10}=4\left(m\right)\)
áp dụng MÔ MEN ta có : \(\Sigma F\backslash\left(G\right)=\Sigma P\backslash\left(G\right)\)
\(\Leftrightarrow F.AC=P.AH\Leftrightarrow F.8=40.4\Leftrightarrow F=\dfrac{40.4}{8}=20\left(N\right)\)
vậy độ lớn của lực \(F\) là \(20\left(N\right)\)
Giải:
- Áp dụng công thức tính trọng lượng: \(P=10.m\)
=> Trọng lượng của thanh sắt là: \(P_{thanh^{_{ }}sắt}\)\(=10.30=300N\)
- Có: lực do đầu A của thanh sắt tác dụng lên giá đỡ là: \(P_1=200N\)
=> Lực do đầu B của thanh sắt tác dụng lên giá đỡ là: \(P_2=P-P_1=300-200=100N\)
- Theo quy tắc hợp hai lực song song cùng chiều, ta có:\(\dfrac{P_1}{P_2}=\dfrac{GB}{GA}\Leftrightarrow\dfrac{GB}{GA}=\dfrac{300}{100}=3\Rightarrow3.GB-GB=0\left(1\right)\)
- Có \(GA+GB=AB=3m\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\), ta có hệ sau: \(\left\{{}\begin{matrix}3GB-GB=0\\GA+GB=3m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}GA=0,75m\\GB=2,25m\end{matrix}\right.\)
- Vậy trọng tâm G của thanh cách đầu A một đoạn 0,75m; cách đầu B một đoạn 2,25m.
Áp dụng điều kiện cân bằng của thanh đối với trục quay tại điểm tiếp xúc với sàn ta có M F = M P
Fl.cos 30 ° = P(l/2).cos 30 ° ⇒ F = P/2 = 100(N)
\
