Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai thời điểm gần nhất mà dây duỗi thẳng là \(\frac{T}{2}=0,5s => T = 1s.\)
\(\lambda = v.T= 20.1=20cm.\)

Đáp án C

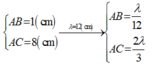
Chọn nút A làm gốc, B và C ở hai bó liền kề và cách nút A nên ta áp dụng công thức:
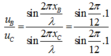
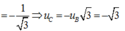
Chú ý: Để có được tỉ số li độ trên ta viết phương trình sóng dừng và lập tỉ của phương trình (27.1) sẽ ra được công thức.
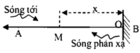
Chọn gốc tọa độ tại O: Nếu sóng tới tại B:
![]()
Thì sóng tại M sẽ có dạng: 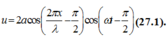
(d: là khoảng cách từ nút đến điểm đang xét).
*Do đó biên dộ dao động: 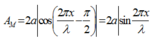
Nếu điểm M cách nút thì công thức tính biên độ: 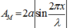
Nếu điểm M cách bụng một khoảng x thì x bằng: ![]()
*Do đó công thức tính biên độ: 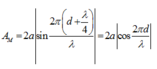

Đáp án C
+ Điều kiện để có sóng dừng trên dây với hai đầu cố định l = n λ 2 với n là số bó sóng hoặc số bụng sóng.
" n = 2 l λ = 2 . 10 2 = 10
" Trên dây có sóng dừng với 10 bụng sóng

Đáp án C
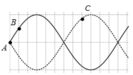
Với bước sóng λ = 12 cm → điểm C và B thuộc hai bó sóng liên tiếp nhau.
→ B và C luôn dao động ngược pha nhau, với hai đại lượng ngược pha, ta luôn có:
u C u B = − a C a B = − sin 2 π A B λ sin 2 π A C λ = sin 2 π .8 12 sin 2 π .1 12 = − 3 → u C = − 3 c m

Chọn D.
Với bức xạ λ vị trí vân sáng bậc k = 3, ta có x k = k λD a . Với bức xạ λ' vị trí vân sáng bậc k', ta có x k ' = k ' λ ' D a . Hai vân sáng này trùng nhau ta suy ra xk = xk’ tương đương với kλ = k’λ’ tính được λ’ = 0,6μm
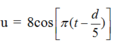
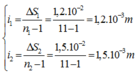
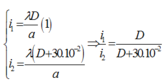
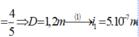
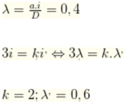


Đáp án: D