K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
8 tháng 4 2021
1.
\(1+tan\alpha+tan^2\alpha+tan^3\alpha\)
\(=1+\dfrac{sin\alpha}{cos\alpha}+\dfrac{sin^2\alpha}{cos^2\alpha}+\dfrac{sin^3\alpha}{cos^3\alpha}\)
\(=1+\dfrac{sin\alpha}{cos\alpha}+\dfrac{sin^2\alpha}{cos^2\alpha}\left(1+\dfrac{sin\alpha}{cos\alpha}\right)\)
\(=\left(\dfrac{sin^2\alpha}{cos^2\alpha}+1\right)\left(1+\dfrac{sin\alpha}{cos\alpha}\right)\)
\(=\dfrac{1}{cos^2\alpha}\left(1+\dfrac{sin\alpha}{cos\alpha}\right)=\dfrac{sin\alpha+cos\alpha}{cos^3\alpha}\)
giúp em với mng!!!
10 tháng 11 2021
\(c,A\left(-2;2\right)\inđths\Leftrightarrow-2a+b=2\left(1\right)\\ Đths//Ox\Leftrightarrow a=0;b=y\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow a=0;b=2\)
NP
0
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
1.
\(\dfrac{1-cosx+cos2x}{sin2x-sinx}=\dfrac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}\)
\(=\dfrac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\dfrac{cosx}{sinx}=cotx\)
2.
\(\dfrac{1+tan^4x}{tan^2x+cot^2x}=\dfrac{1+tan^4x}{tan^2x+\dfrac{1}{tan^2x}}=\dfrac{1+tan^4x}{\dfrac{tan^4x+1}{tan^2x}}=tan^2x\)
3.
\(sin^4x+cos^4x=sin^4x+cos^4x+2sin^2x.cos^2x-2sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-2sin^2x.cos^2x\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
4.
Áp dụng câu 3:
\(sin^4x+cos^4x=1-2sin^2x.cos^2x\)
\(=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2\)
\(=1-\dfrac{1}{2}sin^22x\)
5.
\(sin\left(x+y\right)sin\left(x-y\right)=\dfrac{1}{2}cos\left[\left(x-y\right)-\left(x+y\right)\right]-\dfrac{1}{2}cos\left[\left(x-y\right)+\left(x+y\right)\right]\)
\(=\dfrac{1}{2}\left(cos2y-cos2x\right)=\dfrac{1}{2}\left(1-2sin^2y\right)-\dfrac{1}{2}\left(1-2sin^2x\right)\)
\(=sin^2x-sin^2y\)
6.
\(tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}\)
\(=\dfrac{1}{sinx.cosx}=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)
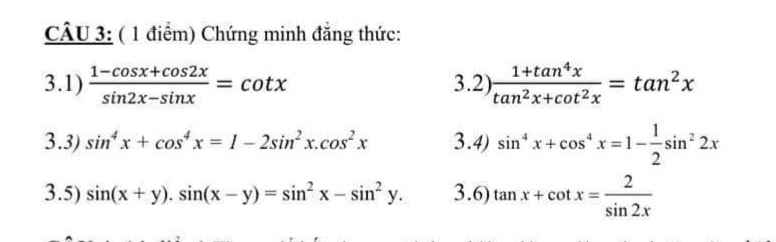
a.
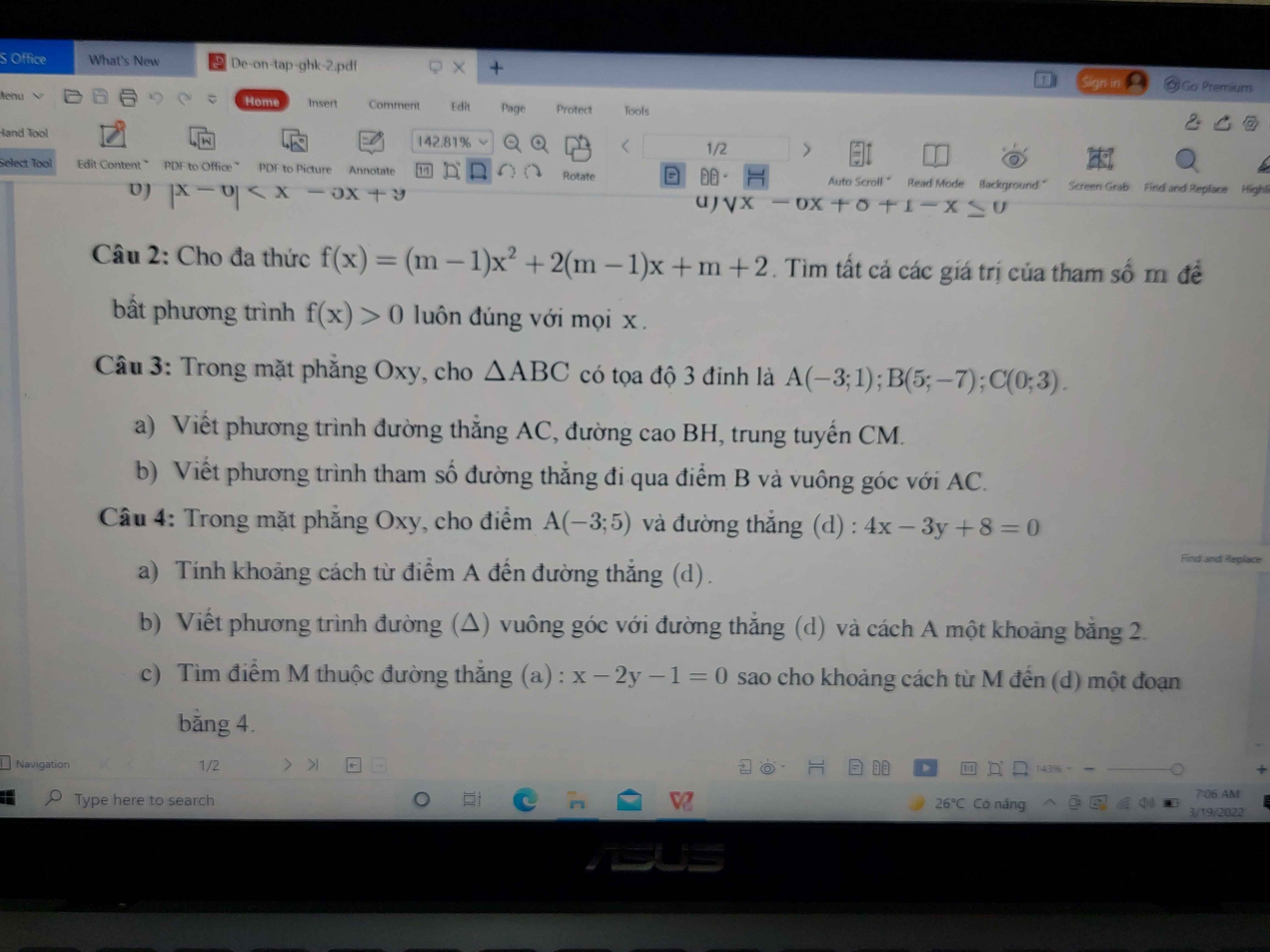
\(d\left(A;d\right)=\dfrac{\left|4.\left(-3\right)-3.5+8\right|}{\sqrt{4^2+\left(-3\right)^2}}=-\dfrac{19}{5}\)
b.
Do \(\Delta\perp d\) nên \(\Delta\) nhận (3;4) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(3x+4y+c=0\)
\(d\left(A;\Delta\right)=2\Leftrightarrow\dfrac{\left|-3.3+4.5+c\right|}{\sqrt{3^2+4^2}}=2\)
\(\Leftrightarrow\left|c+11\right|=10\Rightarrow\left[{}\begin{matrix}c=-21\\c=-1\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}3x+4y-1=0\\3x+4y-21=0\end{matrix}\right.\)
c.
Do \(M\in\left(a\right)\) nên tọa độ có dạng: \(M\left(2m+1;m\right)\)
\(d\left(M;d\right)=\dfrac{\left|4\left(2m+1\right)-3m+8\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)
\(\Leftrightarrow\left|5m+12\right|=20\Rightarrow\left[{}\begin{matrix}m=\dfrac{8}{5}\\m=-\dfrac{32}{5}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(\dfrac{21}{5};\dfrac{8}{5}\right)\\M\left(-\dfrac{59}{5};-\dfrac{32}{5}\right)\end{matrix}\right.\)