K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PM
8
6 tháng 9 2023
\(E=1.1+2.2+3.3+4.4+...+99.99\)
\(\Rightarrow E=1^2+2^2+3^2+4^2+...+99^2\)
\(\Rightarrow E=\dfrac{99.\left(99+1\right)\left(2.99+1\right)}{6}\)
\(\Rightarrow E=\dfrac{99.100.199}{6}\)
\(\Rightarrow E=33.50.199=328350\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 9 2023
E = 1 x 1 + 2 x 2 + 3 x 3 + 4 x 4 +...+ 99 x 99
E = 1x(2-1) + 2 x (3-1)+...+ 99 x (100 -1)
D = 1 x 2 - 1 + 2 x 3 - 2 +...+ 99 x 100 - 99
D = 1x2 + 2 x 3 +...+ 99 x 100 - ( 1 + 2 +...+ 99)
Đặt A = 1x2 + 2 x 3 +...+ 99 x 100
B = 1 + 2 + ...+ 99
1x2 x 3 = 1x2x3
2x3x3 = 2x 3 x (4-1) = 2x3x4 - 1x2x3
3 x 4 x 3 = 3 x 4 x ( 5 - 2) = 3 x 4 x 5 - 2 x 3 x 4
................................................
99 x 100 x 3 = 99 x 100 x (101 - 98) = 99x100x101 - 98 x 99 x 100
Cộng vế với vế ta có: 3A = 99 x 100 x 101
A = 99 x 100 x 101 : 3 = 333300
B = 1 + 2 + 3 + ...+ 99
B = (99 + 1).[(99 -1):1 +1]:2 = 4950
E = 33300 - 4950 = 328350
ND
2
NV
3
BT
1
PC
1
LH
13 tháng 1 2020
xy - x + 2y - 2 = 3
x ( y - 1 ) + 2 ( y - 1 ) = 3
( y - 1 ) ( x + 2 ) = 3
=> y - 1 và x + 2 thuộc Ư ( 3 ) = { - 3; -1; 1; 3 }
Ta có bảng:
| y - 1 | -1 | 1 | 3 | - 3 |
| x + 2 | 3 | - 3 | 1 | - 1 |
| x | 1 | - 5 | - 1 | - 3 |
| y | 0 | 2 | 4 | - 2 |
| TM | TM | TM | TM |
Vậy ...
13 tháng 3 2022
\(3n-2\inƯ\left(15\right)\) \(=\left\{1;-1;3;-3;5;-5;15;-15\right\}.\)
\(\Leftrightarrow n\in\left\{1;\dfrac{1}{3};\dfrac{5}{3};\dfrac{-1}{3};\dfrac{7}{3};-1;\dfrac{17}{3};\dfrac{-13}{3}\right\}.\)
Mà \(n\ne\dfrac{2}{3};n\in Z.\)
\(\Rightarrow n\in\left\{1;-1\right\}.\)
NM
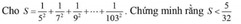
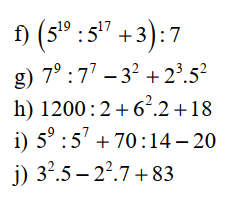giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
1
13 tháng 12 2021
\(f,=\left(5^2+3\right):7=28:7=4\\ g,=7^2-9+8\cdot25=49-9+200=240\\ h,=600+72+18=690\\ i,=5^2+5-20=10\\ j,=45-28+83=100\)
a: Những tia trên hình vẽ là Ex,Ey,Em,En,Ct,CK,Cn
Đoạn thẳng: EK,EC,CK
b: Các cặp tia đối nhau là:
Ex;Ey
Kx;Ky
Cn;CE
CK,Ct