K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MS
0
10 tháng 10 2017
Gọi số cây trồng được của hai lớp 7A và 7B lần lượt là x, y.
Theo bài ra ta có :
\(\frac{x}{y}=\frac{5}{4}\)và y - x = 15
Từ \(\frac{x}{y}=\frac{5}{4}\Rightarrow\frac{x}{5}=\frac{y}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{5}=\frac{y}{4}=\frac{x-y}{5-4}=\frac{15}{1}=15\)
Suy ra:
x = 15 . 5 = 75
y = 15 . 4 = 60
Vậy số cây trồng được của hai lớp 7A và 7B lần lượt là 75 ; 60 (cây)
10 tháng 10 2017
Sửa lại bài của mình làm nha bạn
*Theo bài ra ta có :
\(\frac{x}{y}=\frac{5}{4}\) và x - y = 15
NH
0
L
0
22 tháng 9 2023
(x - 13 + y)2 + (x - 6 - y)2 ≥ 0 + 0 = 0
Vì dấu "=" xảy ra nên x - 13 + y = 0 và x - 6 - y = 0
x + y = 13 và x - y = 6
x = (13 - 6) : 2 = 3,5
y = 13 - 3,5 = 9,5
Vậy x = 3,5 và y = 9,5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 9 2023
(\(x\) - 13 + y)2 + (\(x\) - 6 - y)2 = 0
(\(x\) - 13 + y)2 ≥ 0 ∀ \(x;y\)
(\(x-6-y\))2 ≥ 0 ∀ \(x;y\)
⇒(\(x-13+y\))2 + (\(x\) - 6- y)2 = 0
⇔ \(\left\{{}\begin{matrix}x-13+y=0\\x-6-y=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x-6-y=0\\x-13+y+x-6-y=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}y=x-6\\2x=19\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{19}{2}-6\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{7}{2}\end{matrix}\right.\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 9 2023
(\(x\) -13 +y)2 + (\(x\) - 6 - y)2 = 0
(\(x-13+y\))2 ≥0; (\(x\) - 6 - y)2 ≥ 0∀ \(x;y\)
⇒(\(x-13+y\))2 + (\(x-6-y\))2 = 0
⇔ \(\left\{{}\begin{matrix}x-13+y=0\\x-6-y=0\end{matrix}\right.\)
⇒ -13 - 6 + 2\(x\) = 0 ⇒ \(x\) = \(\dfrac{19}{2}\) ⇒ y = \(\dfrac{19}{2}\) - 6 ⇒ y = \(\dfrac{7}{2}\)
Vậy (\(x\);y) = (\(\dfrac{19}{2}\); \(\dfrac{7}{2}\))
23 tháng 9 2023
\(\left(x-13+y\right)^2+\left(x-6-y\right)^2=0\left(1\right)\)
Ta có :
\(\left\{{}\begin{matrix}\left(x-13+y\right)^2\ge0,\forall x;y\in R\\\left(x-6-y\right)^2\ge0,\forall x;y\in R\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\left(x-13+y\right)^2=0\\\left(x-6-y\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-13+y=0\\x-6-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=19\\y=x-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{19}{2}-6=\dfrac{7}{2}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{7}{2}\end{matrix}\right.\) thoả mãn đề bài
LD
1
1 tháng 11 2018
tập hợp N là số nguyên (1)
mà A = giá tri nguyên (2)
và x < 30 (3)
từ (1),(2),(3) ta có:
x={0;1;2;3;...;29}
KT
30 tháng 9 2018
Đặt \(\frac{x}{4}\)= \(\frac{y}{14}\)= k ( k khác 0 )
=> x = 4k và y = 14k thay vào biểu thức x.y=56 ta có
4k . 14k = 56
56k\(^2\)= 56
k2= 56 :56 = 1
=> k = 1 hoặc k = -1.
Với k=1 khi đó x = 4k = 4.1 =4
y = 14.1 =14
Với k = -1 thì x = -4 và y = -14
vậy x = 4 , y=14 và x = -4, y = -14
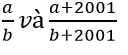
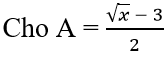
help me
sách nào mới được chứ