QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a)
+) Tỉnh Lai Châu: Xét mẫu số liệu đã sắp xếp là:
\(\begin{array}{*{20}{c}}{14,2}&{14,8}&{18,6}&{18,8}&{20,3}&{21,0}&{22,7}&{23,5}&{23,6}&{24,2}&{24,6}&{24,7}\end{array}\)
Khoảng biến thiên của mẫu số liệu là: \(R = 24,7 - 14,2 = 10,5.\)
Cỡ mẫu là \(n = 12\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 21,85.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(\begin{array}{*{20}{c}}{14,2}&{14,8}&{18,6}&{18,8}&{20,3}&{21,0}\end{array}\). Do đó \({Q_1} = 18,7.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(\begin{array}{*{20}{c}}{22,7}&{23,5}&{23,6}&{24,2}&{24,6}&{24,7}\end{array}\). Do đó \({Q_3} = 23,9\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 23,9 - 18,7 = 5,2\)
+) Tỉnh Lâm Đổng: Xét mẫu số liệu đã sắp xếp là:
\(16,0\;\;16,3\;\;17,4\;\;17,5\;\;18,5\;\;18,6\;\;18,7\;\;19,3\;\;19,5\;\;19,8\;\;20,2\;\;20,3\)
Khoảng biến thiên của mẫu số liệu là: \(R = 20,3 - 16,0 = 4,3.\)
Cỡ mẫu là \(n = 12\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 18,65.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(\begin{array}{*{20}{c}}{16,0}&{16,3}&{17,4}&{17,5}&{18,5}&{18,6}\end{array}\). Do đó \({Q_1} = 17,45.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(\begin{array}{*{20}{c}}{18,7}&{19,3}&{19,5}&{19,8}&{20,2}&{20,3}\end{array}\). Do đó \({Q_3} = 19,65\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 19,65 - 17,45 = 2,2\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Không gian mẫu của phép thử là: \(\Omega {\rm{ }} = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}.\) Vậy \(n\left( \Omega \right) = 4\)
+) Các kết quả thuận lợi cho biến cố A là: \(A{\rm{ }} = {\rm{ }}\left\{ {SS;{\rm{ }}NN} \right\}\). Vậy \(n\left( A \right) = 2\)
+) Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2023
Có \(C_{10}^2\) cách chọn 2 nhóm bất kì (không gian mẫu)
Có 2 biến cố thuận lợi: 1,2 hoặc 3,4
Do đó xác suất là: \(P=\dfrac{2}{C_{10}^2}\)
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Không thể tính n(\(\Omega \)), n(F) và n(G) bằng cách liệt kê ra hết các phần tử của \(\Omega \), F và G rồi kiểm đếm.
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = {\rm{ }}\left\{ {\left( {i,j} \right){\rm{ | }}i,{\rm{ }}j{\rm{ }} = {\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6} \right\}\) trong đó (i,j) là kết quả “Lần thứ nhất xuất hiện mặt i chấm, lần thứ hai xuất hiện mặt j chấm”. Vậy \(n\left( \Omega \right) = 36\)
+) Gọi A là biến cố “Số chấm trong hai lần gieo đều là số nguyên tố”.
Ta có các kết quả thuận lợi cho biến cố A là: (2 ; 2) (2;3) (2;5) (3; 2) (3;3) (3;5) (5;2) (5;3) (5;5). Vậy \(n\left( A \right) = 9\)
+) Vậy xác suất của biến cố A là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{9}{{36}} = \frac{1}{4}\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}\). Vậy \(n\left( \Omega \right) = 4\)
+) Gọi A là biến cố “Có ít nhất một lần xuất hiện mặt sấp”
+) Các kết quả thuận lợi cho biến cố A là: \(SS;{\rm{ }}SN;{\rm{ }}NS\)tức là \(A = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS} \right\}\). Vậy \(n\left( A \right) = 3\).
+) Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{3}{4}\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}\). Vậy \(n\left( \Omega \right) = 4\)
+) Gọi A là biến cố “Kết quả của hai lần tung là khác nhau”.
Các kết quả thuận lợi cho biến cố A là: \(SN;{\rm{ }}NS\)tức là \(A = \left\{ {SN;NS} \right\}\).Vậy \(n\left( A \right) = 2\)
+) Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
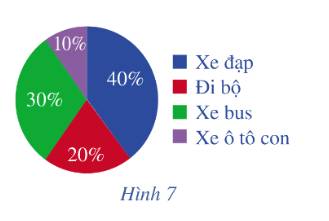
a) Số bạn đi xe đạp đến trường là: \(40.40\% = 16\) ( học sinh )
b) Chọn ngẫu nhiên một bạn để phân công vào đội xung kích của trường từ 40 bạn ta được một tổ hợp chập 1 của 40 phần tử. Do đó, không gian mẫu \(n\left( \Omega \right) = C_{40}^1\)( phần tử)
Gọi A là biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”.
Để chọn 1 bạn học là bạn đến trường bằng xe đạp ta được một tổ hợp chập 1 của 16 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{16}^1\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{16}^1}}{{C_{40}^1}} = \frac{2}{5}\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
Mỗi lần lấy ngẫu nhiên ra 10 bông hoa từ 30 bông hoa ta có một tổ hợp chập 10 của 30. Do đó số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{30}^{10}\) (phần tử)
Gọi A là biến cố “Trong 10 bông hoa được chọn ra có ít nhất một bông màu trắng”
Vậy \(\overline A \) là biến cố “Trong 10 bông hoa được chọn ra đều là hoa màu vàng”
Mỗi cách lấy ra đồng thời 10 bông hoa từ 15 bông hoa màu vàng là một tổ hợp chập 10 của 15 phần tử. Vậy số phần tử của biến cố \(\overline A \) là : \(n\left( {\overline A } \right) = C_{15}^{10}\) ( phần tử)
Xác suất của biến cố \(\overline A \) là: \(P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{1}{{10005}}\)
Xác suất của biến cố A là: \(P\left( A \right) = 1 - P\left( {\overline A } \right) = \frac{{10004}}{{10005}}\)
Do các viên bi có cùng kích thước và trọng lượng nên số kết quả cho việc lấy 2 viên bi từ hộp có 10 viên bi có \(C_{10}^2\) cách
Gọi A là biến cố “Lấy được hai viên bi cùng màu”
Việc lấy được hai viên bi cùng màu có hai khả năng
+) Khả năng thứ nhất: hai viên bi cùng màu xanh có \(C_5^2\) cách
+) Khả năng thứ hai: hai viên bi cùng màu đỏ có \(C_5^2\) cách
Suy ra có \(2C_5^2 = 20\) kết quả thuận lợi cho biến cố A
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{20}}{{C_{10}^2}} = \frac{4}{9}\)
Gọi B là biến cố “Lấy được hai viên bi khác màu”
Việc lấy được hai viên bi khác màu có hai công đoạn
+) Công đoạn thứ nhất: Lấy 1 viên bi màu xanh có \(5\) cách
+) Công đoạn thứ hai: Lấy 1 viên bi màu đỏ có 5 cách
Suy ra có \(5.5 = 25\) kết quả thuận lợi cho biến cố B
Vậy xác suất của biến cố B là: \(P\left( B \right) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{25}}{{C_{10}^2}} = \frac{5}{9}\)