Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(n\left( {\overline E } \right) = n\left( \Omega \right) - n\left( E \right)\).

a) Sơ đồ cây
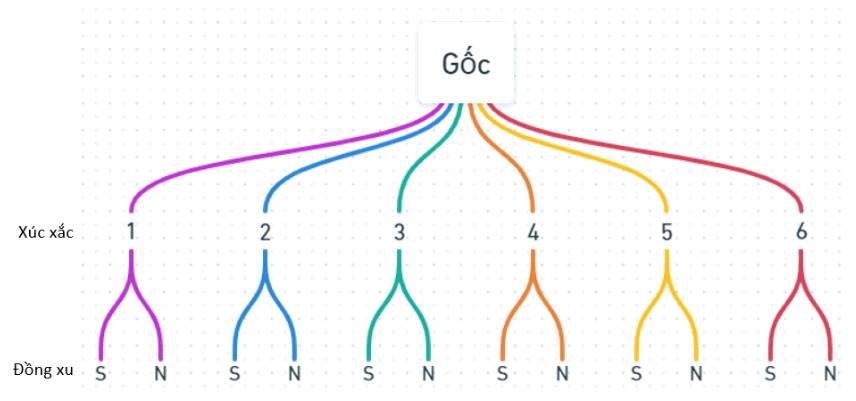
b) Từ sơ đồ cây ta có \(n\left( \Omega \right) = 12\).
Ta có \(F = \left\{ {\left( {1,N} \right);\left( {2,N} \right);\left( {3,N} \right);\left( {4,N} \right);\left( {5,N} \right);\left( {6,N} \right)} \right\}\). Suy ra \(n\left( F \right) = 6\). Vậy \(P\left( F \right) = \frac{6}{{12}} = 0,5\).
\(G = \left\{ {\left( {1,S} \right);\left( {2,S} \right);\left( {3,S} \right);\left( {4,S} \right);\left( {5,S} \right);\left( {6,S} \right);\left( {5,N} \right)} \right\}\). Suy ra \(n\left( G \right) = 7\). Vậy \(P\left( G \right) = \frac{7}{{12}}\).

Gọi n là số trẻ mới sơ sinh. Vận dụng ý nghĩa thực tế của xác suất, ta có \(n.0,488 \approx 10000\).
Vậy \(n \approx 20492\)(trẻ sơ sinh). Do đó, trong 10000 bé gái thì có khoảng \(20492 - 10000 = 10492\)(bé trai).

Tổng số kết quả có thể xảy ra của phép thử là \(n\left( \Omega \right) = {2^4}\)
a) Biến cố đối của biến cố “Xuất hiện ít nhất ba mặt sấp” là biến cố “ Xuất hiện nhiều nhất một mặt sấp”
Biến cố xảy ra khi trên mặt đồng xu chỉ xuất hiện một hoặc không có mặt sấp nào. Số kết quả thuận lợi cho biến cố là \(C_4^1 + 1 = 5\)
Xác suất của biến cố là \(P = \frac{5}{{{2^4}}} = \frac{5}{{16}}\)
b) Biến cố đối của biến cố “Xuất hiện ít nhất một mặt ngửa” là biến cố “ Không xuất hiện mặt ngửa nào”
Biến cố xảy ra khi tất cả các mặt đồng là mặt sấp. Chỉ có 1 kết quả thuận lợi cho biến cố
Xác suất của biến cố là \(P = \frac{1}{{{2^4}}} = \frac{1}{{16}}\)

Bạn ghi lại đề đi bạn. Với lại cho mình hỏi là đề bài yêu cầu gì vậy?

Không thể tính n(\(\Omega \)), n(F) và n(G) bằng cách liệt kê ra hết các phần tử của \(\Omega \), F và G rồi kiểm đếm.