Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tọa độ M là:
1/2x=-1/2x+2 và y=1/2x
=>x=2 và y=1
Tọa độ N là:
1/2x=-1/2x+6 và y=1/2x
=>x=6 và y=3
Tọa độ P là:
1/2x-4=-1/2x+2
=>x=6 và y=1/2*6-4=3-4=-1
Tọa độ Q là:
1/2x-4=-1/2x+6 và y=1/2x-4
=>x=10 và y=1/2*10-4=5-4=1
M(2;1); N(6;3); P(6;-1); Q(10;1)
\(\overrightarrow{NM}=\left(-4;-2\right)\)
\(\overrightarrow{QP}=\left(-4;-2\right)\)
Vì vecto NM=vecto QP
nên MNPQ là hình bình hành

Lời giải:
PT hoành độ giao điểm của đường thẳng thứ nhất và thứ hai:
\(2x-5-\left (-\frac{1}{2}x+\frac{5}{2}\right)=0\)
\(\Leftrightarrow \frac{5}{2}x-\frac{15}{2}=0\leftrightarrow x=3\)
\(\Rightarrow \) Giao điểm \((3;1)\)
Tương tự, ta cũng thu được giao điểm giữa phương trình đường thẳng thứ hai và ba, đường thẳng thứ nhất và thứ ba đều là \((3;1)\)
Vậy ba đường thẳng này giao nhau ở cùng một điểm, do đó chúng cắt nhau không thể tạo thành một tam giác .

c: =>3x^2+3y^2=39 và 3x^2-2y^2=-6
=>5y^2=45 và x^2=13-y^2
=>y^2=9 và x^2=4
=>\(\left\{{}\begin{matrix}x\in\left\{2;-2\right\}\\y\in\left\{3;-3\right\}\end{matrix}\right.\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x}=5\\\sqrt{x}-\sqrt{y}=-\dfrac{11}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y}=1+\dfrac{11}{2}=\dfrac{13}{2}\end{matrix}\right.\)
=>x=1 và y=169/4
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x+3-3}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x+2-2}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{3}{x+1}-\dfrac{2}{y+4}=4-3=1\\-\dfrac{2}{x+1}-\dfrac{5}{y+4}=9-2=7\end{matrix}\right.\)
=>x+1=11/9 và y+4=-11/19
=>x=2/9 và y=-87/19

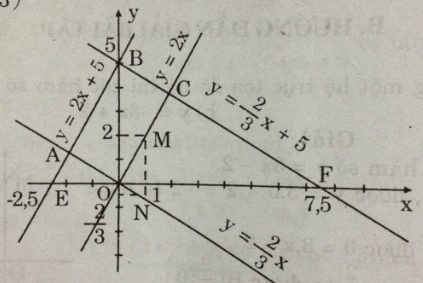
b)Bốn đường thẳng đã cho cắt nhau tại các điểm O, A.
Vì đường thẳng y = 2x + 5 song song với đường thẳng y = 2x, đường thẳng y = - 2x/3 +5 song song với đường thẳng y = - 2x/3 , tứ giác OABC là hình bình hành (có hai cặp cạnh song song).
Vậy tứ giác OABC là hình bình hành







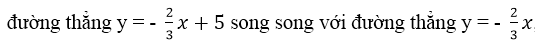

cắt nhau tại tung độ 5