Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

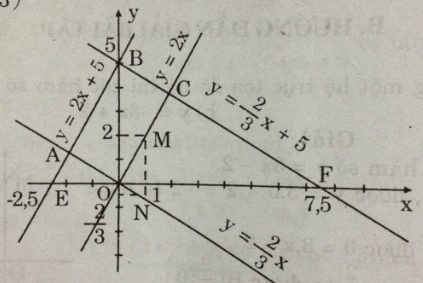
b)Bốn đường thẳng đã cho cắt nhau tại các điểm O, A.
Vì đường thẳng y = 2x + 5 song song với đường thẳng y = 2x, đường thẳng y = - 2x/3 +5 song song với đường thẳng y = - 2x/3 , tứ giác OABC là hình bình hành (có hai cặp cạnh song song).
Vậy tứ giác OABC là hình bình hành

câu a đề đúng là:
a) Vẽ đồ thị hàm số (D): y = \(-\dfrac{5}{3}x+2\)
b: (d3): y=4x-2+4=4x+2
=>(D1)//(D3); (D2) cắt (D1) và (D2) cắt (D3)

Bây giờ ta sẽ đi tìm tọa độ giao điểm của 3 đường thẳng trên
Với (d1) và (d2) cắt nhau tại điểm \(A\left(x_1;y_1\right)\) nên khi đó:
\(\hept{\begin{cases}y_1=3x_1-2\\y_1=-\frac{1}{3}x_1+\frac{4}{3}\end{cases}}\Rightarrow3x_1-2=-\frac{1}{3}x_1+\frac{4}{3}\Leftrightarrow\frac{10}{3}x_1=\frac{10}{3}\Rightarrow\hept{\begin{cases}x_1=1\\y_1=1\end{cases}}\)
Vậy \(A\left(1;1\right)\)
Tương tự gọi B,C là giao điểm của đường (d3) với (d2) , (d1)
Khi đó ta dễ dàng tính được: \(B\left(4;0\right)\) ; \(C\left(2;4\right)\)
Áp dụng công thức tính khoảng cách giữa 2 điểm trong mặt phẳng ta có:
\(AB=\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}=\sqrt{10}\Rightarrow AB^2=10\)
\(AC=\sqrt{\left(1-2\right)^2+\left(1-4\right)^2}=\sqrt{10}\Rightarrow AC^2=10\)
\(BC=\sqrt{\left(4-2\right)^2+\left(0-4\right)^2}=\sqrt{20}\Rightarrow BC^2=20\)
Xét tam giác ABC có: \(\hept{\begin{cases}AB=AC\\AB^2+AC^2=BC^2\left(=20\right)\end{cases}}\)
=> Tam giác ABC vuông cân tại A
=> đpcm
giao điểm của d1 với d2 là : y=3x-2
y=-1/3x+4/3
<=> 3x -2 =-1/3+4/3
y=3x-2
<=> x=1
y=1
vaaky giao điểm của d1 và d2 có tọa độ A(1,1)
tương tự ta được giao điểm của: d2 với d3 có tọa độ B (4,0)
d3 với d1 có tọa độ C(2,4)
độ dài AB là\(\sqrt{\left(Xa-Xb\right)^2+\left(Ya+Yb\right)^2}\)=\(\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}\)=\(\sqrt{10}\)
tương tư ta được AC= \(\sqrt{10}\)
=> AB=AC ; d1 vuông góc d2 vì 3.(-1/3)=-1
=> tam giác ABC VUÔNG CÂN

c: =>3x^2+3y^2=39 và 3x^2-2y^2=-6
=>5y^2=45 và x^2=13-y^2
=>y^2=9 và x^2=4
=>\(\left\{{}\begin{matrix}x\in\left\{2;-2\right\}\\y\in\left\{3;-3\right\}\end{matrix}\right.\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x}=5\\\sqrt{x}-\sqrt{y}=-\dfrac{11}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y}=1+\dfrac{11}{2}=\dfrac{13}{2}\end{matrix}\right.\)
=>x=1 và y=169/4
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x+3-3}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x+2-2}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{3}{x+1}-\dfrac{2}{y+4}=4-3=1\\-\dfrac{2}{x+1}-\dfrac{5}{y+4}=9-2=7\end{matrix}\right.\)
=>x+1=11/9 và y+4=-11/19
=>x=2/9 và y=-87/19

Tọa độ M là:
1/2x=-1/2x+2 và y=1/2x
=>x=2 và y=1
Tọa độ N là:
1/2x=-1/2x+6 và y=1/2x
=>x=6 và y=3
Tọa độ P là:
1/2x-4=-1/2x+2
=>x=6 và y=1/2*6-4=3-4=-1
Tọa độ Q là:
1/2x-4=-1/2x+6 và y=1/2x-4
=>x=10 và y=1/2*10-4=5-4=1
M(2;1); N(6;3); P(6;-1); Q(10;1)
\(\overrightarrow{NM}=\left(-4;-2\right)\)
\(\overrightarrow{QP}=\left(-4;-2\right)\)
Vì vecto NM=vecto QP
nên MNPQ là hình bình hành

Giải hệ sau :
Câu a :
\(\left\{{}\begin{matrix}x+y=-1\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\-x=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\x=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
Vậy ...........................
Câu b :
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\dfrac{1}{y}=b\end{matrix}\right.\) . Ta có :
\(\left\{{}\begin{matrix}a+b=\dfrac{1}{5}\\3a+4b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{3}{5}\\3a+4b=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-b=-\dfrac{7}{5}\\3a+4b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{7}{5}\\a=-\dfrac{6}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{7}{5}\\\dfrac{1}{y}=-\dfrac{6}{5}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{7}\\y=-\dfrac{5}{6}\end{matrix}\right.\)
Vậy..................
\(a,\left\{{}\begin{matrix}2x-y=4\\x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=4\\2x+10y=6\end{matrix}\right.\left\{{}\begin{matrix}11y=2\\2x+10y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{11}\\2x+10.\dfrac{2}{11}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{11}\\2x=\dfrac{46}{11}\end{matrix}\right.\left\{{}\begin{matrix}y=\dfrac{2}{11}\\x=\dfrac{23}{11}\end{matrix}\right.\)

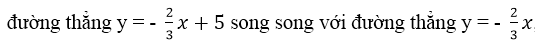




Lời giải:
PT hoành độ giao điểm của đường thẳng thứ nhất và thứ hai:
\(2x-5-\left (-\frac{1}{2}x+\frac{5}{2}\right)=0\)
\(\Leftrightarrow \frac{5}{2}x-\frac{15}{2}=0\leftrightarrow x=3\)
\(\Rightarrow \) Giao điểm \((3;1)\)
Tương tự, ta cũng thu được giao điểm giữa phương trình đường thẳng thứ hai và ba, đường thẳng thứ nhất và thứ ba đều là \((3;1)\)
Vậy ba đường thẳng này giao nhau ở cùng một điểm, do đó chúng cắt nhau không thể tạo thành một tam giác .