Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Áp dụng công thức độc lập, ta có: \(A^2 = x^2+\frac{v^2}{\omega^2} \Rightarrow\) \(8^2+\frac{12^2}{\omega^2} = 6^2+\frac{16^2}{\omega^2} \Rightarrow \omega = 2 \ (rad/s) \Rightarrow f = \frac{1}{\pi} \ Hz\)

Sau đây là keys
1/ \(A.T=2\pi\sqrt{\dfrac{m}{k}}\)
2/ \(D.\) Cộng hưởng cơ
3/ \(\varphi_1-\varphi_2=\pi+2k\pi=\left(2k+1\right)\pi\Rightarrow A.\left(2k+1\right)\pi\)
4/ \(\omega=2\pi f\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{\pi}{2\pi}=\dfrac{1}{2}\left(Hz\right)\Rightarrow A.0,5Hz\)
5/ \(A.\) Cơ năng, biên độ, tần số
6/ Câu này vẽ đường tròn ra là xong thôi
\(\varphi=arc\cos\left(\dfrac{3}{6}\right)+\dfrac{\pi}{2}+arc\sin\left(\dfrac{3\sqrt{3}}{6}\right)=\dfrac{\pi}{3}+\dfrac{\pi}{2}+\dfrac{\pi}{3}=\dfrac{7\pi}{6}\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{7\pi}{6.4\pi}=\dfrac{7}{24}\left(s\right)\Rightarrow A.\dfrac{7}{24}\left(s\right)\)
7/ \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}k\dfrac{4}{9}A^2\Rightarrow\dfrac{W_t}{W}=\dfrac{\dfrac{2}{9}kA^2}{\dfrac{1}{2}kA^2}=\dfrac{4}{9}\Leftrightarrow W_t=\dfrac{4}{9}W\left(J\right)\)
\(\Rightarrow W_d=W-W_t=W-\dfrac{4}{9}W=\dfrac{5}{9}W\left(J\right)\Rightarrow B.\dfrac{5}{9}W\left(J\right)\)
Câu này em nghĩ nên cho thêm đơn vị Jun ạ!
8/ \(T-mg\cos\alpha=m.a_{ht}=\dfrac{mv^2}{l}\)
\(\Leftrightarrow T=mg\cos\alpha+2mg\left(\cos\alpha-\cos\alpha_0\right)\)
\(\Leftrightarrow T=mg\left(3\cos\alpha-2\cos\alpha_0\right)\)
Lực căng cực đại khi vật ở vị trí thấp nhất
\(\Rightarrow\alpha=0\Rightarrow T_{max}=mg\left(3.1-2\cos60^0\right)=2mg\left(N\right)\)
Lực căng cực tiểu khi vật ở vị trí ban đầu
\(\Rightarrow\alpha=60^0\Rightarrow T_{min}=mg\left(3.\dfrac{1}{2}-2.\dfrac{1}{2}\right)=0,5mg\left(N\right)\)
\(\Rightarrow\dfrac{T_{max}}{T_{min}}=\dfrac{2}{0,5}=4\Rightarrow D.4\)

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

\(A^2 = x^2+\frac{v^2}{\omega ^2}=4^2 +\frac{9,42^2}{(2.\pi.0,5)^2} = 25\)
=> \(A \approx 5 cm \approx 0,05 m.\)
Lực phục hồi cực đại: \(F _{max}=kA = m(2\pi f)^2.A= 0,5.4.10.0,5^2.(0,05)= 0,25N.\)



Đáp án D
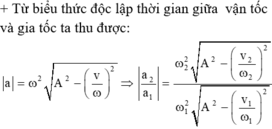
+ Từ biểu thức độc lập thời gian giữa vận tốc và gia tốc ta thu được:
a = ω 2 A 2 − v ω 2
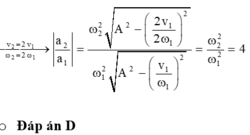
⇒ a 2 a 1 = ω 2 2 A 2 − v 2 ω 2 2 ω 1 2 A 2 − v 1 ω 1 2 → ω 2 = 2 ω 1 v 2 = 2 v 1 a 2 a 1 = ω 2 2 A 2 − 2 v 1 2 ω 1 2 ω 1 2 A 2 − v 1 ω 1 2 = ω 2 2 ω 1 2 = 4