
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(20\sqrt{300}-15\sqrt{675}+5\sqrt{75}\right):\sqrt{15}\\ \Leftrightarrow A=\left(200\sqrt{3}-225\sqrt{3}+25\sqrt{3}\right):\sqrt{15}\\ \Leftrightarrow A=0:\sqrt{15}=0\)
\(B=\left(\sqrt{325}-\sqrt{117}+2\sqrt{208}\right):\sqrt{13}\\ \Leftrightarrow B=\left(5\sqrt{13}-3\sqrt{13}+8\sqrt{13}\right):\sqrt{13}\\ \Leftrightarrow B=10\sqrt{13}:\sqrt{13}=10\)
c: Ta có: \(C=\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+\sqrt{162}}\)
\(=\dfrac{-2\left(\sqrt{3}-2\sqrt{2}\right)}{\sqrt{6}\left(\sqrt{3}-2\sqrt{2}\right)}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{6}\left(\sqrt{5}+\sqrt{27}\right)}\)
\(=\dfrac{-3}{\sqrt{6}}=-\dfrac{\sqrt{6}}{2}\)

1,
Dễ thấy MN,MP,NP là đtb tg ABC
Do đó \(NP^2=\dfrac{BC^2}{4}=\dfrac{AB^2+AC^2}{4}=\dfrac{AB^2}{4}+\dfrac{AC^2}{4}=MN^2+MP^2\)
Vậy tg MNP vuông tại M
Do đó tg MNP nt đg tròn tâm I là trung điểm NP
Dễ cm ANMP là hcn
Do đó ANMP nt
Do đó A cũng nằm trên đg tròn tâm I hay đg tròn đi qua 3 điểm M,N,P còn đi qua điểm A
Ai đồ tự làm đi

\(\tan C=\dfrac{AB}{AC}=\dfrac{15}{6}\approx\tan68^0\)
Vậy \(\widehat{C}\approx68^0\)


2: \(AB\cdot\cos B+AC\cdot\cos C\)
\(=AB\cdot\dfrac{AB}{BC}+AC\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB^2+AC^2}{BC}=BC\)

Câu 11:
a: =x^2-x-5x+5
=(x-1)(x-5)
b: \(=x^5+x^4+x^3-x^4-x^3-x^2+x^2+x+1\)
=(x^2+x+1)(x^3-x^2+1)
c: \(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+96\)
=(x^2+7x+6)(x^2+7x+16)
=(x+1)(x+6)(x^2+7x+16)


Hàng ngày bố Lâm đạp xe đạp từ nhà đến trường để đón con.Bao jo ông cũng đến trường vừa kịp lúc Lâm ra khỏi trường.Một hôm ,Lâm tan học sớm hơn 45 phút ,em đi bộ về luôn giữa đường gặp bố đến đón.Bố liền em về nhà và sớm hơn mọi ngày 30phut.hỏi
a)Lâm đi bộ trong bao lâu
b)so sánh vận tốc xe đạp và vận tốc Lâm
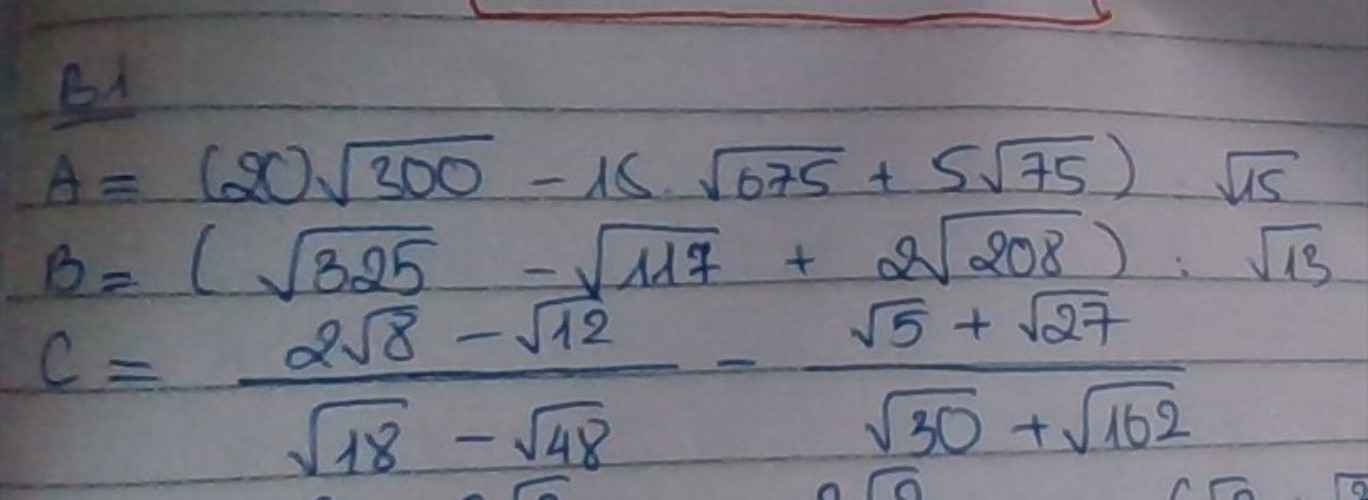
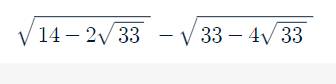 Cíu mình dới mn ơi huhu
Cíu mình dới mn ơi huhu
