Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d: Xét ΔABK và ΔCKB có
AB=CK
KB chung
AK=CB
Do đó: ΔABK=ΔCKB

\(x^2\left(x^2-4\right)=3\left(x^2-4\right)\)
\(\Rightarrow x^2\left(x^2-4\right)-3\left(x^2-4\right)=0\)
\(\Rightarrow\left(x^2-4\right)\left(x^2-3\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x^2-4=0\\x^2-3=0\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}\left[\begin{array}{nghiempt}x=2\\x=-2\end{array}\right.\\\left[\begin{array}{nghiempt}x=\sqrt{3}\\x=-\sqrt{3}\end{array}\right.\end{array}\right.\)
Vậy x=2; x= - 2 ; x=\(\sqrt{3}\) ; x=\(-\sqrt{3}\)
Có : \(x^2\left(x^2-4\right)=3\left(x^2-4\right)\)
\(\Leftrightarrow x^2\left(x^2-4\right)-3\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2-4=0\\x^2-3=0\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x^2=4\\x^2=3\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=2;x=-2\\x=\sqrt{3};x=-\sqrt{3}\end{array}\right.\)
Vậy \(x=-2;x=2;x=-\sqrt{3};x=\sqrt{3}\)


Ta có : \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4};a^2-b^2+2c^2\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a^2-b^2+2c^2}{2^2-3^2+2.4^2}=\frac{108}{27}=4\)
\(\Leftrightarrow\frac{a}{2}=4\Rightarrow a=8\)
\(\Leftrightarrow\frac{b}{3}=4\Rightarrow b=12\)
\(\Leftrightarrow\frac{c}{4}=4\Rightarrow c=16\)
Vậy a = 8

Tự vẽ hình nha
Xét \(\Delta ADBvà\Delta AED\)
AE=AB(giả thiết)
\(\widehat{BAD}=\widehat{EAD}\)(Giả thiết)
Cạnh AD chung
\(\Rightarrow\Delta ADB=\Delta AED\left(c-g-c\right)\)

Câu 2:
\(1.f\left(x\right)=2x^3+x^2-3x+9.\\ g\left(x\right)=-2x^3-x^2+3.\)
Câu 3:
1. Ta có: \(AB=AC\) (\(\Delta ABC\) cân).
Mà \(AC=IC\left(gt\right). \)
\(\Rightarrow AB=IC.\)
Ta có: \(\widehat{ABC}=\widehat{ACB}\) (\(\Delta ABC\) cân).
Mà \(\widehat{ACB}=\widehat{ICE}\) (đối đỉnh).
\(\Rightarrow\widehat{ABC}=\widehat{ICE}.\)
Hay \(\widehat{ABD}=\widehat{ICE}.\)
Xét \(\Delta ABD\) và \(\Delta ICE:\)
BD = CE (gt).
\(\widehat{ABD}=\widehat{ICE}\left(cmt\right).\)
AB = IC (cmt).
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right).\)
2. Xét \(\Delta BDM\) và \(\Delta CEN:\)
\(\widehat{MBD}=\widehat{NCE}\left(\widehat{ABD}=\widehat{ICE}\right).\)
\(BD=CE\left(gt\right).\)
\(\widehat{BDM}=\widehat{CEN}\left(=90^o\right).\)
\(\Rightarrow\Delta BDM=\Delta CEN\left(g-c-g\right).\)
\(\Rightarrow BM=CN\) (2 cạnh tương ứng).

\(\frac{17^2}{x}=\frac{7x^2}{-119}\)
=\(17^2.\left(-119\right)=7x^2.x\)
=\(-34391=7x^3\)
=\(-4913=x^3\)
x=\(\sqrt[3]{-4913}=-17\)

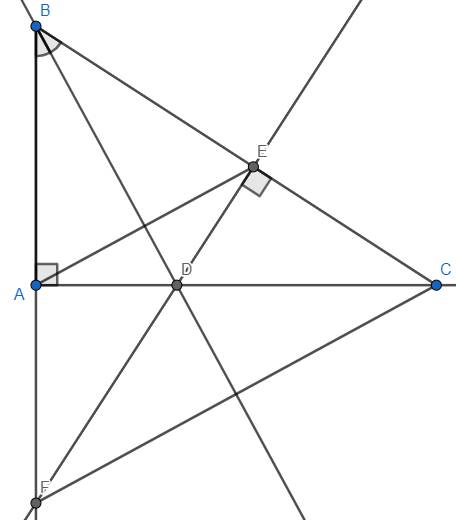
c) Ta đã biết DA = DE (chứng minh trên) (1)
Trong tam giác EDC vuông tại E có DC đối diện đỉnh E
Suy ra DC là cạnh lớn nhất trong tam giác EDC
Hay DC > DE (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC

Xét \(\Delta ABC\)có \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\Delta ABC\)cân tại A
\(\Rightarrow AB=AC\)
Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AB=AC\)
\(\widehat{B}=\widehat{C}\)
\(\widehat{AHB}=\widehat{AHC}\)( \(DoAH\perp BC\))
\(\Rightarrow\Delta AHB=\Delta AHC\)(CẠNH HUYỀN - GÓC NHỌN)
do AH vuông góc với BC ( gt) => GÓC AHB = 90 ĐỘ , góc AHC = 90 độ
xét tam giác ABH và ACH có:
góc B = góc C ( GT )
AH : cạnh chung
GÓC AHB = AHC ( cm trên )
nên tam giác ahb = ahc

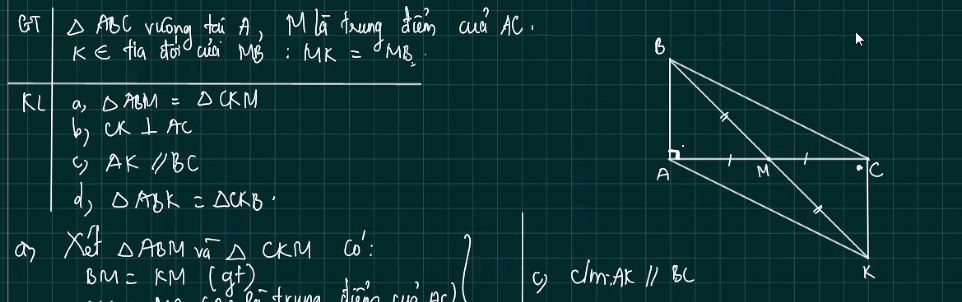 giúp mình câu d với
giúp mình câu d với