Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét △BAH vuông tại H có: HBA + BAH = 90o (tổng 2 góc nhọn trong △vuông)
Ta có: BAC = BAH + HAC => BAH + HAC = 90o
=> HBA = HAC => HBA = KAD
Xét △HBA vuông tại H và △KAD vuông tại K
Có: HBA = KAD (cmt)
AB = AD (gt)
=> △HBA = △KAD (ch-gn)
b, Vì BC ⊥ AH (gt) => HE ⊥ HK
và AH ⊥ KD (gt) => HK ⊥ KD
=> HE // KD (từ vuông góc đến song song)
Xét △HKD vuông tại K và △DEH vuông tại E
Có: HD là cạnh chung
KHD = HDE (HE // KD)
=> △HKD = △DEH (ch-gn)
c, Vì △HKD = △DEH (cmt)
=> KD = EH (2 cạnh tương ứng)
Mà AH = KD (△HBA = △KAD)
=> AH = EH
https://h.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+c%C3%A2n+t%E1%BA%A1i+A.+K%E1%BA%BB+AH+vu%C3%B4ng+g%C3%B3c+BC+t%E1%BA%A1i+H++a)+CM+tam+gi%C3%A1c+ABH=tam+gi%C3%A1c+ACH++b)+V%E1%BA%BD+trung+tuy%E1%BA%BFn+BM.+G%E1%BB%8Di+G+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AH+v%C3%A0+BM.+Ch%E1%BB%A9ng+minh+G+l%C3%A0+tr%E1%BB%8Dng+t%C3%A2m+c%E1%BB%A7a+tam+gi%C3%A1c+ABC++c)+Cho+AB=30cm,+BH=18cm.+T%C3%ADnh+AH,AG++d)+T%E1%BB%AB+H+k%E1%BA%BB+HD+song+song+v%E1%BB%9Bi+AC(D+thu%E1%BB%91c+AB),+ch%E1%BB%A9ng+minh+ba+%C4%91i%E1%BB%83m+C,G,D+th%E1%BA%B3ng+h%C3%A0ng&id=248109
a, xét tam giác ABH à tg ACH có AH chung
^BAH = ^CAH do AH là pg
AB = AC (gt)
=> tg ABH = tg ACH (c-g-c)
b, tg ABH = tg ACH (câu a )
=> ^AHC = ^AHB
mà ^AHC + ^AHB = 180
=> ^AHC = 90
=> AH _|_ BC
c, xét tam giác ADH và tam giác AEH có : AE chung
^ADH = ^AEH = 90
^bah = ^cah
=> Tg ADH= tg AEH (ch-gn)
=> AE = AD
=> tg AED cân tại A => ^ADE = (180 - ^BAC) : 2
tg ABC cân tại A => ^ABC = (180 - ^bac) : 2
=> ^ade = abc
mà ^ade đồng vị ^abc
=> de // bc
a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
b: BH=CH=6cm
=>AH=8cm
c: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAHE cân tại A
hay AE=AH
d: Xét ΔADH có
AI là đường cao
AI là đườngtrung tuyến
Do đó:ΔADH cân tại A
=>AD=AH=AE
=>ΔADE cân tại A
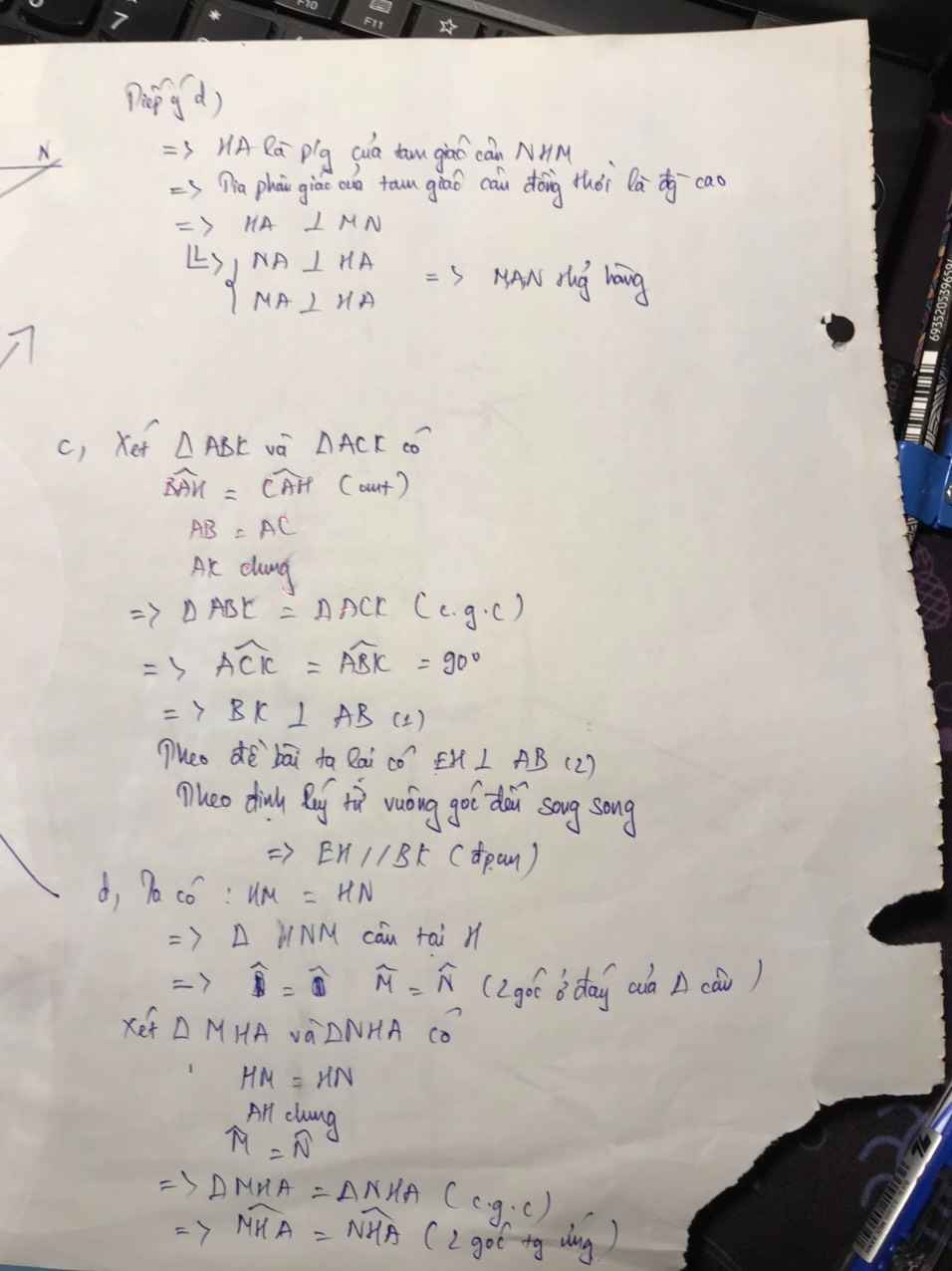
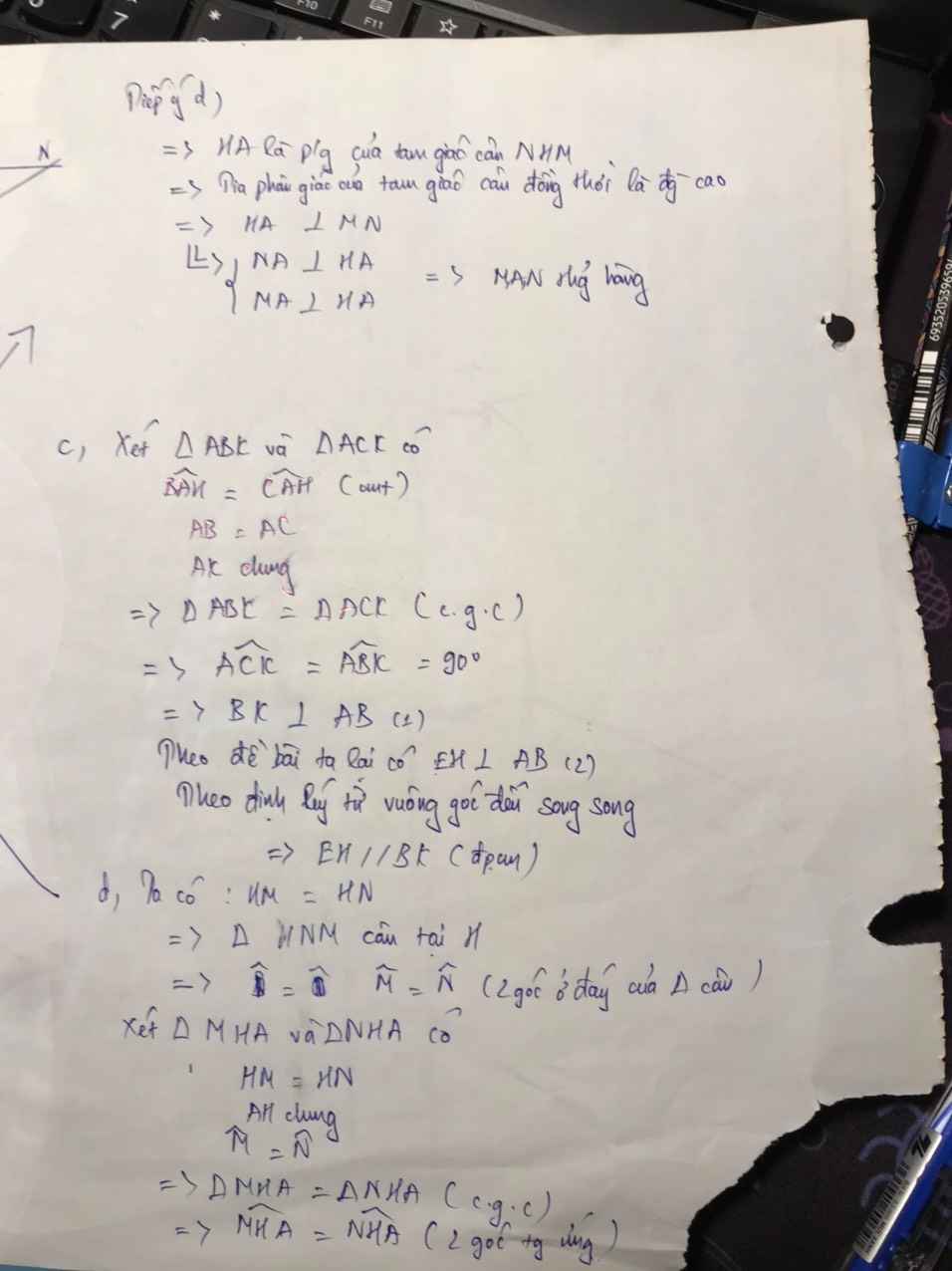
Xét \(\Delta ABC\)có \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\Delta ABC\)cân tại A
\(\Rightarrow AB=AC\)
Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AB=AC\)
\(\widehat{B}=\widehat{C}\)
\(\widehat{AHB}=\widehat{AHC}\)( \(DoAH\perp BC\))
\(\Rightarrow\Delta AHB=\Delta AHC\)(CẠNH HUYỀN - GÓC NHỌN)
do AH vuông góc với BC ( gt) => GÓC AHB = 90 ĐỘ , góc AHC = 90 độ
xét tam giác ABH và ACH có:
góc B = góc C ( GT )
AH : cạnh chung
GÓC AHB = AHC ( cm trên )
nên tam giác ahb = ahc