Giải phương trình nghiệm dương: \(x^3+y^3-9xy=0\).

\(x^3+y^3-9xy=0\).

">

K

Khách

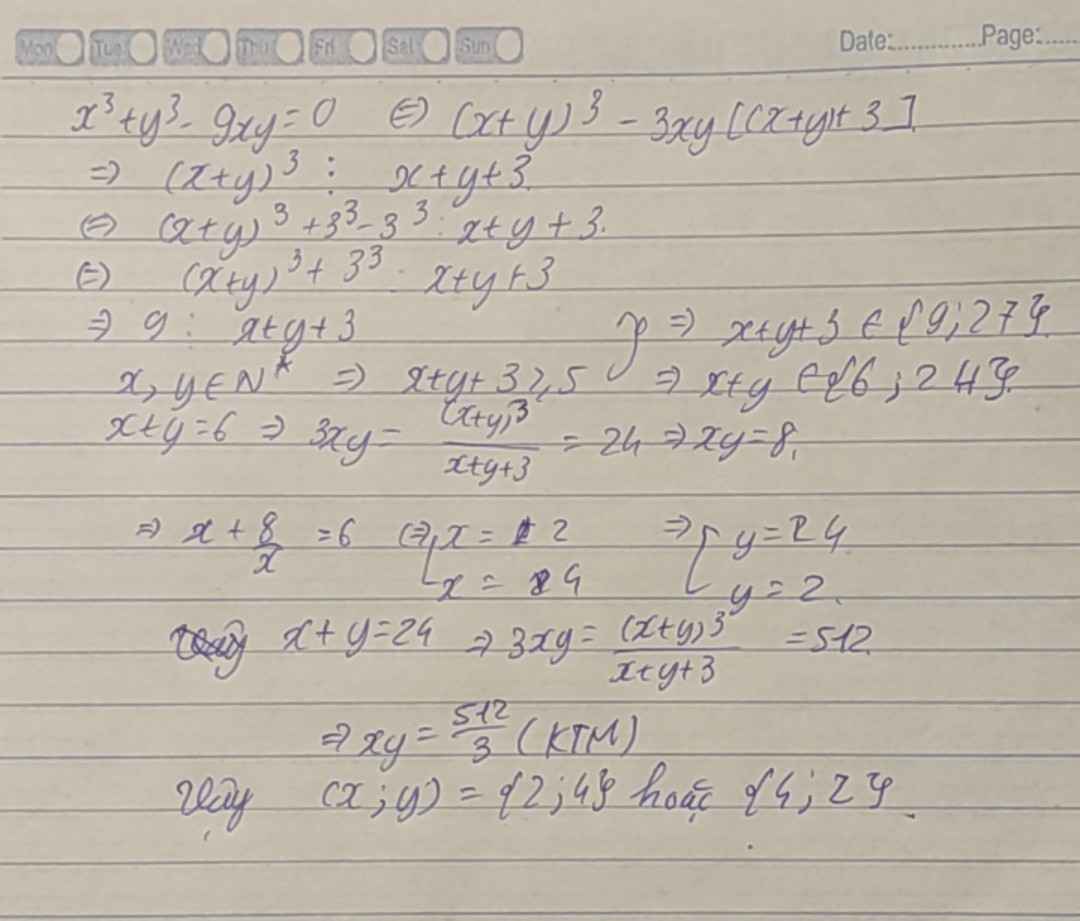
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

LY

Lee Yeong Ji

3 tháng 5 2022

Giải phương trình nghiệm dương: \(x^3+y^3-9xy=0\).

#Hỏi cộng đồng OLM #Toán lớp 9

1

AA

Almoez Ali

3 tháng 5 2022

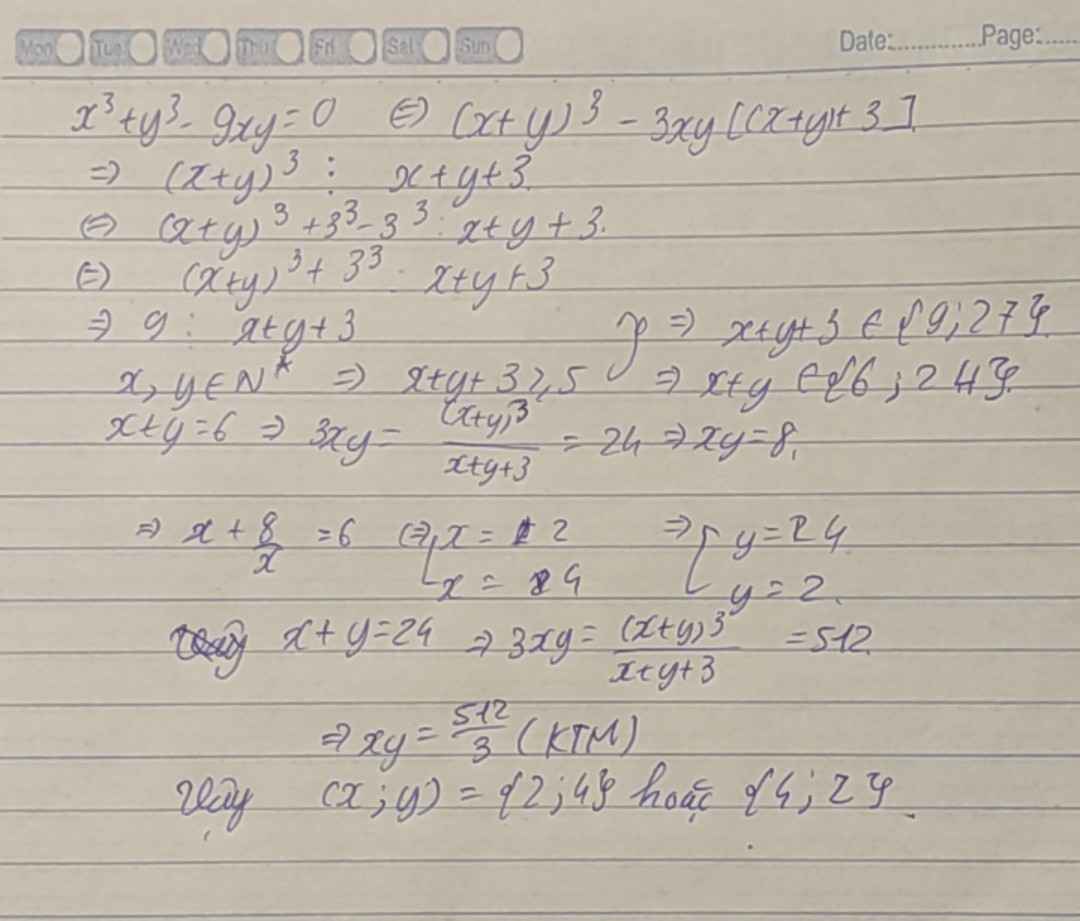
undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

TT

Trương Tuấn Nghĩa

4 tháng 9 2017 - olm

Giải pt nghiệm nguyên: \(x^{^3}-9xy+y^3=0\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

DH

Đức Hiếu Nguyễn

9 tháng 1 2019 - olm

Giải phương trình nghiệm nguyên dương sau:

\(1!+2!+3!+...+x!=y^3\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

NT

Nguyễn Trung Hiếu

8 tháng 1 2017 - olm

Giải phương trình nghiệm nguyên dương:
a) \(\frac{1}{x}+\frac{1}{y}=\frac{1}{3}\)
b)\(2^x+3^x=5^x\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

NH

Ngọc Hạnh Nguyễn

15 tháng 3 2018 - olm

tìm (x,y) nguyên dương thỏa \(x^3+y^3-9xy=0\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

NV

Nhóc vậy

18 tháng 12 2017 - olm

Gọi a là nghiệm dương của phương trình: \(\sqrt{2}x^2+x-1=0\), không giải phương trình tính giá trị của

\(C=\frac{2a-3}{\sqrt{2\left(2a^4-2a+3\right)}+2a^2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

0

DN

Diệp Nhi

9 tháng 2 2020 - olm

Giúp mk với. Mk đang cần gấp. Thank trước nha

Giải hệ phương trình sau:

\(\hept{\begin{cases}x^3-6x^2y+9xy^2-4y^3=0\\\sqrt{x-y}+\sqrt{x+y}=2\end{cases}}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

NP

Nguyễn Phương Thảo

9 tháng 2 2020

\(\hept{\begin{cases}x^3-6x^2y+9xy^2-4y^3=0\left(1\right)\\\sqrt{x-y}+\sqrt{x+y}=2\left(2\right)\end{cases}}\)

ĐKXĐ: \(x\ge y\ge0\)

ta có: (1)\(\Leftrightarrow\left(x^3-y^3\right)-3y^3-9x^2y+3x^2y+9xy^2=0\)

\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)+3y\left(x^2-y^2\right)-9xy\left(x-y\right)=0\)

\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2+3y\left(x+y\right)-9xy\right)=0\)

\(\Leftrightarrow\left(x-y\right)\left(x^2-5xy+4y^2\right)=0\)

\(\orbr{\begin{cases}x=y\\x^2-5xy+4y^2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=y\\\left(x-y\right)\left(x-4y\right)=0\end{cases}}}\)\(\Leftrightarrow\orbr{\begin{cases}x=y\\x=4y\end{cases}}\)

* Thay x=y vào phương trình (2), ta được: \(\sqrt{y-y}+\sqrt{2y}=2\Leftrightarrow y=2\Rightarrow x=y=2\)

* thay x=4y vào phương trình (2), ta được: \(\sqrt{4y-y}+\sqrt{4y+y}=2\)

\(\Leftrightarrow y=8-2\sqrt{15}\)\(\Rightarrow x=32-8\sqrt{15}\)

Vậy.......

NV

Nhóc vậy

17 tháng 12 2017 - olm

Gọi a là nghiệm dương của phương trình: \(\sqrt{2}x^2+x-1=0\). Không giải phương trình hãy tính giá trị của

\(C=\frac{2a-3}{\sqrt{2\left(2a^4-2a+3\right)}+2a^2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

DC

Đặng công quý

18 tháng 12 2017

Thay \(\sqrt{2}a^2=1-a\ge\)0 suy ra a <=1 tính được mẫu = \(-\sqrt{2}\left(2a-3\right)\)

DN

Diệp Nguyễn Thị Huyền

6 tháng 8 2021 - olm

Gọi a là nghiệm dương của phương trình : \(\sqrt{2}x^2+x-1=0\). Không giải phương trình, hãy tính giá trị của biểu thức :

\(C=\frac{2a-3}{\sqrt{2\left(2a^4-2a+3\right)}+2a^2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

NM

Nguyễn Minh Quang

Giáo viên

6 tháng 8 2021

ta có :

\(\sqrt{2}a^2+a-1=0\Leftrightarrow\sqrt{2}a^2=1-a\) nên ta có \(a\le1\)

\(\Rightarrow2a^4=a^2-2a+1\)Vậy \(C=\frac{2a-3}{\sqrt{2\left(a^2-4a+4\right)}+2a^2}=\frac{2a-3}{2a^2+\sqrt{2}\left(2-a\right)}=\frac{2a-3}{\sqrt{2}\left(\sqrt{2}a^2-a+2\right)}\)

\(=\frac{2a-3}{\sqrt{2}\left(1-a-a+2\right)}=\frac{2a-3}{\sqrt{2}\left(3-2a\right)}=-\frac{1}{\sqrt{2}}\)

NH

Ngọc Hạnh

15 tháng 3 2018

tìm (x,y) nguyên dương thỏa \(x^3+y^3-9xy=0\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

AH

Akai Haruma

Giáo viên

15 tháng 3 2018

Lời giải:

Ta có: \(x^3+y^3-9xy=0\)

\(\Leftrightarrow (x+y)^3-3xy(x+y)-9xy=0\)

\(\Leftrightarrow (x+y)^3=9xy+3xy(x+y)\)

\(\Leftrightarrow (x+y)^3=3xy[(x+y)+3]\)

\(\Rightarrow (x+y)^3\vdots x+y+3\)

\(\Leftrightarrow (x+y)^3+3^3-3^3\vdots x+y+3\)

Theo phân tích hằng đẳng thức: \((x+y)^3+3^3\vdots x+y+3\)

Suy ra \(3^3\vdots x+y+3(1)\)

Vì \(x,y\in\mathbb{N}^*\Rightarrow x+y+3\geq 5(2)\)

Từ \((1);(2)\Rightarrow x+y+3\in\left\{9;27\right\}\)

\(\Rightarrow x+y\in\left\{6;24\right\}\)

Nếu \(x+y=6\Rightarrow 3xy=\frac{(x+y)^3}{x+y+3}=24\Rightarrow xy=8\)

Áp dụng hệ thức Viete suy ra $x,y$ là nghiệm của PT: \(X^2-6X+8=0\)

\(\Rightarrow (x,y)=(2,4)\) và hoán vị

Nếu \(x+y=24\Rightarrow 3xy=\frac{(x+y)^3}{x+y+3}=512\Rightarrow xy=\frac{512}{3}\not\in\mathbb{N}\) (loại)

Vậy \((x,y)=(2,4)\) và hoán vị