K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
0
NT
2
26 tháng 4 2019
Ta có: \(a^2+b^2+c^2>2\left(a+b+c\right)\)
\(\Leftrightarrow\) \(a^2+b^2+c^2+3>2\left(a+b+c\right)\) (Vì 3>0)
\(\Leftrightarrow\) \(a^2+b^2+c^2-2a-2b-2c+3>0\)
\(\Leftrightarrow\) \(\left(a^2-2a+1\right)\)+\(\left(b^2-2b+1\right)\)+\(\left(c^2-2c+1\right)\) \(>0\)
\(\Leftrightarrow\) \(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2>0\) (luôn đúng \(\forall a,b,c\))
Vậy \(\forall a,b,c\) thì \(a^2+b^2+c^2>2\left(a+b+c\right)\)
5 tháng 11 2021
\(a,\Leftrightarrow\left(x^2+2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)+\dfrac{3}{4}=0\\ \Leftrightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}=0\\ \Leftrightarrow\left(x+\dfrac{3}{2}\right)^2=-\dfrac{3}{4}\left(vô.lí\right)\\ \Leftrightarrow x\in\varnothing\\ b,\Leftrightarrow\left(2x-5\right)\left(2x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{5}{2}\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 7 2023
c) \(\dfrac{x+5}{x^2-5x}-\dfrac{x-5}{2x^2+10x}=\dfrac{x+25}{2x^2-50}\)
\(\Leftrightarrow\dfrac{x+5}{x\left(x-5\right)}-\dfrac{x-5}{2x\left(x+5\right)}=\dfrac{x+25}{2\left(x^2-25\right)}\)
\(\Leftrightarrow\dfrac{2\left(x+5\right)\left(x-5\right)}{2x\left(x+5\right)\left(x-5\right)}-\dfrac{\left(x-5\right)^2}{2x\left(x+5\right)\left(x-5\right)}=\dfrac{\left(x+25\right)x}{2x\left(x+5\right)\left(x-5\right)}\)
\(\Leftrightarrow2\left(x^2-25\right)-\left(x^2-10x+25\right)=x^2+25x\)
\(\Leftrightarrow2x^2-50-x^2+10x-25=x^2+25x\)
\(\Leftrightarrow2x^2-x^2-x^2+10x-25x=50+25\)
\(\Leftrightarrow-15x=75\)
\(\Leftrightarrow x=\dfrac{75}{-15}\)
\(\Leftrightarrow x=-5\)
MH
5 tháng 2 2022
\(\dfrac{x+1}{x+2}-\dfrac{5}{x-2}=\dfrac{20}{4-x^2}\) (\(ĐK:x\)≠\(2;-2\))
⇔ \(\dfrac{\left(x+1\right)\left(x-2\right)-5\left(x+2\right)}{x^2-4}=\dfrac{20}{4-x^2}\)
⇔ \(-\left(x+1\right)\left(x-2\right)+5\left(x+2\right)=20\)
⇔ \(-\left(x^2-2x+x-2\right)+5x+10=20\)
⇔ \(-x^2+x+2+5x+10-20=0\)
⇔ \(-x^2+6x-8=0\)
⇔ \(-\left(x^2-6x+9\right)=-1\)
⇔ \(\left(x-3\right)^2=1\)
⇔ \(\left[{}\begin{matrix}x-3=1\\x-3=-1\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
Vậy ...
5 tháng 2 2022
b: \(\Leftrightarrow20-5\left(3x+2\right)>4\left(x+7\right)\)
=>20-15x-10>4x+28
=>-15x+10-4x-28>0
=>-19x-18>0
=>-19x>18
hay x<-18/19
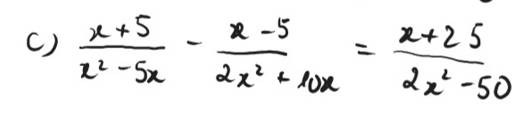
180x-17^2=-272
180x=-272+289=17
x=180/17
180'x-289+272=0
180x-289=0-272
180x-289=-272
180x=-272+289
180x=17
x=17÷180
x=17/180