Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

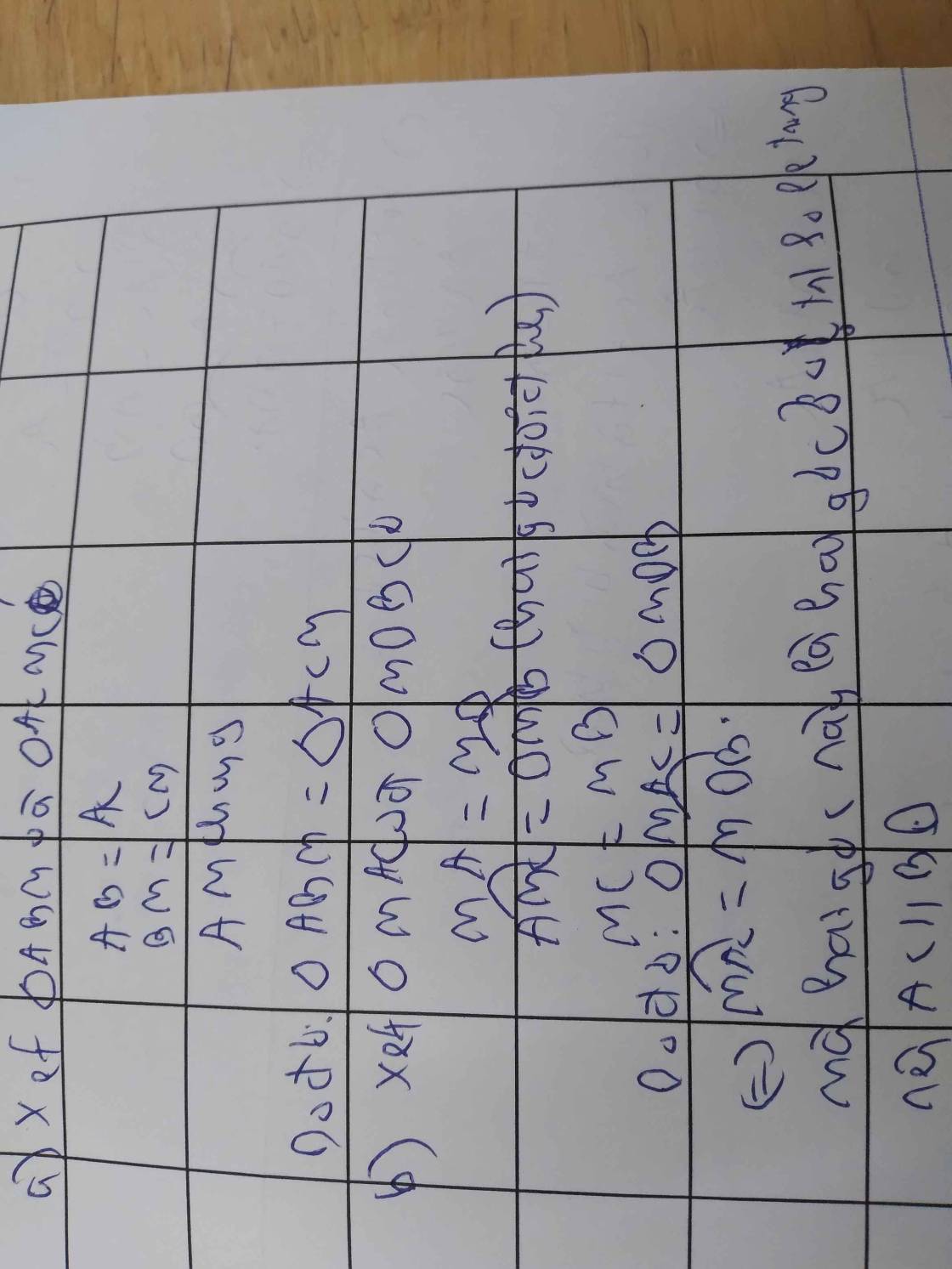
a/ - AB = AC ( gt )
ABM = ACM vì { - AM chung
(c.c.c) - MB = MC ( m là trung điểm )
b/ AB // DC k phải AB // BC
T/g ABM = t/g DCM ( c.g.c)
AM = DM ( gt )
Góc AMB = DMC ( đđ )
BM = CM ( gt )
Có ABM = DCM ( t/g ABM = t/g DCM )
Lại ở vị trí slt
=> AB // DC
c/
AB = AC ( gt )
=> ABC cân tại A
Có AM là trung tuyến ( m là trug điểm )
=> AM là đường cao ABC
=> AM vuông góc BC

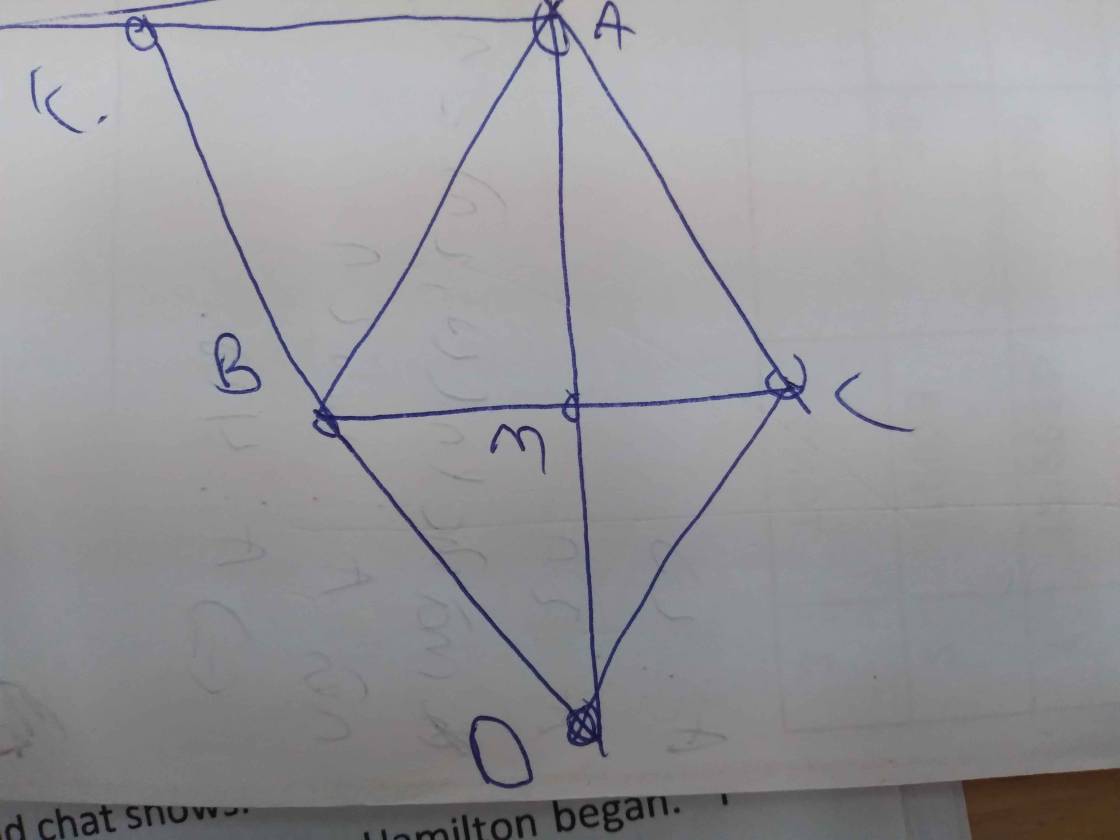
A B C M D
a) Xét tam giác MAB và tam giác MDC có:
MA=MD (gt)
MB=MC( M là trung điểm BC)
\(\widehat{AMB}=\widehat{DMC}\)( đối đỉnh)
=> Tam giác MAB = tam giác MDC
b)
Tam giác MAB = tam giác MDC => \(\widehat{BAM}=\widehat{CDM}\)
Mà hai góc này ở vị trí so le trong
=> AB//CD
c) Ta có AB vuông AC
mag CD // AB
=> CD vuông AC
=> góc ACD bằng 90 độ

Em tham khảo tại đây nhé.
Câu hỏi của Cả cuộc đời này tôi sẽ mãi yêu một người - Toán lớp 7 - Học toán với OnlineMath

a) Sửa đề: ΔAMB=ΔDMC
Xét ΔAMB và ΔDMC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)

Sửa đề: c. AC//BD
a. AB=AC => \(\Delta ABC\)cân tại A => \(\widehat{B}\)= \(\widehat{C}\)
\(\Delta ACM\)và \(\Delta ABM\)có:
- AB = AC (giả thiết)
- Góc B = Góc C (Chứng minh trên)
- MC = MB (M là trung điểm của BC)
nên \(\Delta ACM\)= \(\Delta ABM\)(c.g.c)
Vậy .....
b. \(\Delta ACM\)và \(\Delta DBM\)có:
-AM = DM (giả thiết)
-góc AMC = góc BMD (đối đỉnh)
- MC = MB (lí do như câu a)
nên ....... = ........ (c.g.c)
=> AC = DB (hai cạnh tương ứng)
Vậy .....
c. \(\Delta ACM\)= \(\Delta DBM\)
=> Góc ACM = góc MBD (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Suy ra AC//BD
Vậy ...
Chúc bạn học tốt!

\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB=AC,` \(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABM` và Tam giác `ACM:`
`AB=AC (CMT)`
\(\widehat{B}=\widehat{C}\)
`MB=MC (g``t)`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`b,` Xét Tam giác `AMB` và Tam giác `CMD:`
`AM=MD (g``t)`
\(\widehat{AMB}=\widehat{CMD}\) `( \text {2 góc đối đỉnh})`
`MB = MC (g``t)`
`=> \text {Tam giác AMB = Tam giác CMD (c-g-c)}`
`->`\(\widehat{ABC}=\widehat{DCB}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong
`-> \text {AB // CD}`
`c,` Vì Tam giác `AMB =` Tam giác `CMD (b)`
`-> AB=CD (\text {2 cạnh tương ứng})`
Mà `AB = AC (a)`
`-> AC = CD`
Xét Tam giác `ACD: AC = CD`
`-> \text {Tam giác ACD cân tại C}`