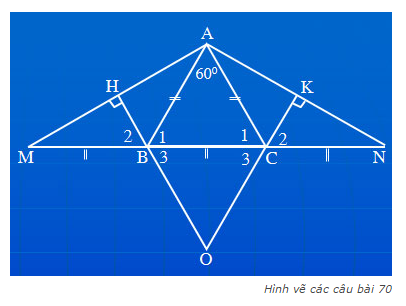
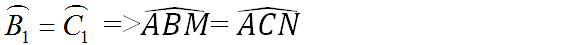Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hoàng Thị Ngọc Anh, chú tuổi gì, Thiên Thảo, Guyo, Mai Linh, Phạm Thái Dương, Lưu Thùy Dung, Nguyễn Văn Toàn, Hoa Thiên Lý, Sky SơnTùng, Nguyễn Thái Bình, Akai Haruma, Nhã Doanh, Phạm Nguyễn Tất Đạt, ngonhuminh, Mashiro Shiina, ,Nguyễn Minh Hùng, Nguyễn Thanh Hằng, nguyen thi vang, Phùng Khánh Linh, kuroba kaito, Nguyễn Huy Tú, Hoàng Lê Bảo Ngọc, Trần Việt Linh, Võ Đông Anh Tuấn, Phương An, Ace Legona, soyeon_Tiểubàng giải,...

a, Vì BE là đường trung tuyến
=>EC=EA
Xét ∆ABE và ∆CKE có :
AE=CE(cmt)
E1=E2(đối đỉnh)
EB=EK(GT)
=∆ABE = ∆CKE(c-g-c)
b,Xét ∆ECN vuông ở N có : C1+E1 = 90 độ
Xét ∆AME vuông ở M có : A1+E1 = 90 độ
Mà E1=E2
=>C1=A1
Xét ∆ECN và ∆AME có :
C1=A1(cmt)
EC=EA(cmt)
E1=E2(đối đỉnh)
=>∆ECN=∆AME(g-c-g)
=>AM=CN
c/ Trong ΔBCK có:
BC+CK > BK ( BĐT tg)
=> BC+CK > 2BE
Mà CK=AB( ΔABE= ΔCKE)
=> AB+BC > 2BE
⇒AB+BC/2>BE

Bạn tham khảo tại đây nhé: Câu hỏi của nhất sông núi .
Chúc bạn học tốt!

Hình như bài này là bai 71,72 gì đó ở SGK 7ở gần cuối trang thì phải

a: Xét ΔBAH vuong tại A và ΔBMH vuông tại M có
BH chung
góc ABH=góc MBH
Do đó: ΔBAH=ΔBMH
b: Ta có: BA=BM
HA=HM
Do đó: BH là đường trung trực của AM
hay BH vuông góc với AM
c: Xét ΔAHN vuong tại A và ΔMHC vuông tại M có
HA=HM
góc AHN=góc MHC
Do đó: ΔAHN=ΔMHC
Suy ra: AN=MC
Xét ΔBNC có BA/AN=BM/MC
nên AM//CN